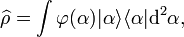Nonclassical light

From Wikipedia, the free encyclopedia

Nonclassical light is light that cannot be described using classical electromagnetism; its characteristics are described by the quantized electromagnetic field and quantum mechanics. Nonclassical light has nonclassical noise properties called quantum noise, which can be understood on the basis of quantum optics.

Common described forms of nonclassical light are the following:

  • Squeezed light exhibits reduced noise in one quadrature component. The most familiar kinds of squeezed light have either reduced amplitude noise or reduced phase noise, with increased noise of the other component.
  • Fock states (also called photon number states) have a well-defined number of photons (stored e.g. in a cavity), while the phase is totally undefined.

Glauber–Sudarshan P representation

Main article: Glauber–Sudarshan P representation

It has been shown that the density matrix for any state of light can be written as:

\widehat {\rho }=\int \varphi (\alpha )|{\alpha }\rangle \langle {\alpha }|{\rm {{d}^{2}\alpha ,}}

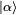where \scriptstyle |\alpha \rangle is a coherent state. A classical state of light is one in which 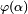\scriptstyle \varphi (\alpha )\, is a probability density function. If it is not, the state is said to be nonclassical.[1]

Aspects of 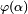\scriptstyle \varphi (\alpha )\, that would make it nonclassical are:

The matter is not quite simple. According to Mandel and Wolf: "The different coherent states are not [mutually] orthogonal, so that even if \scriptstyle P(\alpha )\, behaved like a true probability density [function], it would not describe probabilities of mutually exclusive states."[1]

References

Citations

  1. ↑ 1.0 1.1 Mandel & Wolf 1995, p. 541

Citation bibliography

Mandel, L.; Wolf, E. (1995), Optical Coherence and Quantum Optics, Cambridge UK: Cambridge University Press, ISBN 0-521-41711-2 

General references

  • R. J. Glauber, “Coherent and incoherent states of the radiation field”, Phys. Rev. 131 (6), 2766 (1963)

External links


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.