Nichols algebra
In algebra, the Nichols algebra of a braided vector space (with the braiding often induced by a finite group) is a braided Hopf algebra which is denoted by 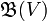 and named after the mathematician Warren Nichols. It takes the role of quantum Borel part of a pointed Hopf algebra [1] such as a quantum groups and their well known finite-dimensional truncations. Nichols algebras can immediately be used to write down new such quantum groups by using the Radford biproduct[1]
and named after the mathematician Warren Nichols. It takes the role of quantum Borel part of a pointed Hopf algebra [1] such as a quantum groups and their well known finite-dimensional truncations. Nichols algebras can immediately be used to write down new such quantum groups by using the Radford biproduct[1]
Susan Montgomory asked[2] to classify which finite groups admit at all finite dimensional indecomposable Nichols algebras over k = C. The answering of this question, moreover the classification of all such Nichols algebras and even all associated quantum groups (see Application) is recently progressing rapidly, although still much is open: The case of an abelian group has been solved 2005,[3] but otherwise this phenomenon seems to be a very rare occasion, with a handful examples known and powerful negation criteria established (see below).
The finite dimensional theory is greatly governed by a theory of root systems and Dynkin diagrams, strikingly similar to those of semisimple Lie algebras.[2] A comprehensive introduction is found in the lecture of Heckenberger [4]
Definition
Consider a Yetter–Drinfeld module V in the Yetter–Drinfeld category  . This is especially a braided vectorspace, see Braided monoidal category.
. This is especially a braided vectorspace, see Braided monoidal category.
The tensor algebra TV of a Yetter–Drinfeld module 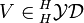 is always a Braided Hopf algebra. The coproduct Δ of TV is defined in such a way that the elements of V are primitive, that is
is always a Braided Hopf algebra. The coproduct Δ of TV is defined in such a way that the elements of V are primitive, that is
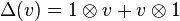 for all v in V.
for all v in V.- The counit ε: TV → k then satisfies the equation ε(v) = 0 for all v in V.
As an example, all universal envelopings of Lie algebras are (trivially braided) quotients thereof for 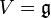 by Serre relations: The basis consists of derivational elements (=primitives), the higher powers usually solemnly of higher derivations and there are no further quotients still preserving V ("universal"). In the braided context, the "true" enveloping turns out to be often much smaller:
by Serre relations: The basis consists of derivational elements (=primitives), the higher powers usually solemnly of higher derivations and there are no further quotients still preserving V ("universal"). In the braided context, the "true" enveloping turns out to be often much smaller:
(note that in the further development of the theory, see below, the Nichols algebra takes rather the role of the quantum Borel part of the enveloping!)
- There are three equivalent characterizations, as proven by W. Nichols around 1978 [5] (better source ? see discussion) They essentially means, that the "superfluous elements" in the braided Hopf algebra TV are exactly corresponding to "extra-primitives" arrising in higher degree, and are exactly detected by all partial skew-derivations being zero "as if it were a constant".
Definition I: Universal quotient
Let 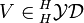 . There exists a largest ideal of TV with the following properties:
. There exists a largest ideal of TV with the following properties:
-
- (hence I is also a coideal) One has
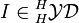 , and the quotient TV/I is a braided Hopf algebra in
, and the quotient TV/I is a braided Hopf algebra in  , the Nichols algebra. It is the "smallest" braided Hopf algebra containing V as a primitive elements (a-priori among others, but see below!)
, the Nichols algebra. It is the "smallest" braided Hopf algebra containing V as a primitive elements (a-priori among others, but see below!)
Definition II: Prescribed primitives
There's a unique braided Hopf algebra, generated by V being primitives, which contains no other primitive elements. It is as well the Nichols algebra.
Definition III: Skew derivatives
Chosen a homogeneous basis 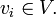 (i.e. coaction/graduation
(i.e. coaction/graduation  ) one may define skew derivations
) one may define skew derivations 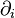 , using the universal property of the tensor algebra:
, using the universal property of the tensor algebra:
Then the Nichols algebra is the quotient of TV by the largest homogeneous ideal which contains no constants and is invariant under all derivations 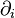 .
.
Examples
We give examples of finite dimensional Nichols algebras. Over characteristic p, this effect already may appear in the non-braided situation, namely the truncated universal envelopings of p-restricted Lie algebras. In characteristic zero and with a braiding coming from an abelian group, this seems to be a similarly frequent occurrence (however more involved, see Classification). For G nonabelian on the other side, only very few examples are known so far, and powerful negation criteria exclude many groups at all (see Classification).
1-dimensional examples
As a first example, consider the 1-dimensional Yetter–Drinfeld module  over the Group Hopf algebra H = k[Z/2Z] with the Cyclic group multiplicatively denoted (as usual in algebra) and generated by some g.
over the Group Hopf algebra H = k[Z/2Z] with the Cyclic group multiplicatively denoted (as usual in algebra) and generated by some g.
- Take as H-coaction (resp. Z/2Z-graduation) on
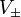 :
: 
- Take as H-action (resp. Z/2Z-action) on
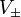 :
: 
- Thus the braiding is
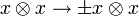
Then, depending on the sign choice, the Nichols algebras are:
Note that the first is as expected (the non-braided case), while the second has been truncated to the point that it's finite dimensional! Similarly, Vq over a higher cyclic group with g acting by some q in k has Nichols algebra ![{\mathfrak {B}}(V_{q})=k[x]/(x^{n})](/2014-wikipedia_en_all_02_2014/I/media/7/f/1/0/7f1079a01a81ee9d871a182d002d9958.png) if q ≠ 1 is a primitive n-th root of unity, and
if q ≠ 1 is a primitive n-th root of unity, and ![{\mathfrak {B}}(V_{q})=k[x]](/2014-wikipedia_en_all_02_2014/I/media/9/f/a/2/9fa228e44c9e9e31b9446b61bd3010ea.png) otherwise.
otherwise.
(from a physical perspective, the V+ corresponds to a boson, while V– represents a fermion restricted by Pauli exclusion principle; an analogy that repeats when considering braided commutators, being (anti)commutators in these cases, see also Supersymmetry as a quantum group and discussion)
Higher-rank examples over G abelian: braided commutators
The next examples show the interaction of two basis elements: Consider the two-dimensional Yetter–Drinfeld module V0,1 = kx ⊕ ky over the group Hopf algebra H = k[Z/2Z × Z/2Z] with the Klein four group multiplicatively denoted and generated by some g,h.
- Take as H-coaction/graduation on V0,1:
 and
and 
- Take as H-action (resp. Z/2Z-action) on V0,1:
-

-
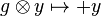
-
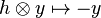
-
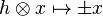 with "+" for V0 (symmetric) and "–" for V1 (asymmetric)
with "+" for V0 (symmetric) and "–" for V1 (asymmetric)
-
- Thus the braiding is
-
Then, depending on the sign choice, the Nichols algebras are of dimension 4 and 8 (they appear in the classification under 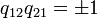 ):
):
There one can see the striking resemblance to Semisimple Lie algebras: In the first case, the braided commutator [x, y] (here: anticommutator) is zero, while in the second, the root string is longer [x, [x, y]] = 0. Hence these two belong to Dynkin diagrams 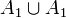 and A2.
and A2.
 |
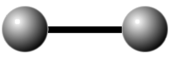 |
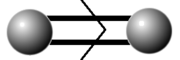
One also constructs examples with even longer root strings V2, V3 corresponding to Dynkin diagrams B2, G2 (but as well no higher ones).
 |
 |
Known examples over G nonabelian
Only a handful of finite dimensional Nichols algebras over k = C are known so far. It is known that in this case each irreducible Yetter–Drinfeld module ![{\mathcal {O}}_{{[g]}}^{\chi }](/2014-wikipedia_en_all_02_2014/I/media/8/3/a/5/83a56ef3883c962666ac8139c3a1d669.png) corresponds to Conjugacy class of the group (together with an irreducible representation of the centralizer of g). An arbitrary Yetter–Drinfeld module is a direct sum of such
corresponds to Conjugacy class of the group (together with an irreducible representation of the centralizer of g). An arbitrary Yetter–Drinfeld module is a direct sum of such ![{\mathcal {O}}_{{[g]}}^{\chi }](/2014-wikipedia_en_all_02_2014/I/media/8/3/a/5/83a56ef3883c962666ac8139c3a1d669.png) , the number of summands is called rank; each summand corresponds to anode in the Dynkin diagram (see below). Note that for the abelian groups as above, the irreducible summands are 1-dimensional, hence rank and dimension coinncide!
, the number of summands is called rank; each summand corresponds to anode in the Dynkin diagram (see below). Note that for the abelian groups as above, the irreducible summands are 1-dimensional, hence rank and dimension coinncide!
| Group G | Conjugacy class | Dimension of V | Dimension of 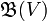 | Source |
|---|---|---|---|---|
Symmetric group 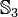 | ![{\mathcal {O}}_{{[(12)]}}\;](/2014-wikipedia_en_all_02_2014/I/media/a/7/d/e/a7de572a0e4a1d32fb82a43603dd55a5.png) |
3 | 12 | [5] |
Symmetric group 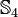 | ![\qquad {\mathcal {O}}_{{[(12)]}}\;](/2014-wikipedia_en_all_02_2014/I/media/d/a/f/9/daf96aa4fe14ac5e409b6c72dc609360.png) |
6 | 576 | [5] |
Symmetric group 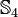 | ![\qquad {\mathcal {O}}_{{[(1234)]}}\;](/2014-wikipedia_en_all_02_2014/I/media/f/d/5/f/fd5fe5a111d51fc03239821ab75ce6af.png) |
6 | 576 | [6] |
Symmetric group 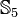 | ![\qquad {\mathcal {O}}_{{[(12)]}}\;](/2014-wikipedia_en_all_02_2014/I/media/d/a/f/9/daf96aa4fe14ac5e409b6c72dc609360.png) |
10 | 8294400 | [5][7] |
Dihedral group 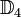 | ![\qquad {\mathcal {O}}_{{[ab]}}\oplus {\mathcal {O}}_{{[b]}}](/2014-wikipedia_en_all_02_2014/I/media/2/9/b/1/29b101ad85142f464755fbfd5a2ce4dc.png) |
4 | 64 | [5] |
Some more examples are found e.g. in the "zoo" on M. Grana's Webpace page[8] (please add more information, see discussion).
Recently, a family of A2 example of rank 2 over extensions of 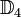 has been constructed[9]
has been constructed[9]
Classification
the following section could use more details. Please add to it, see discussion
Over abelian groups
The Nichols algebras of finite dimension over abelian groups in k = C were classified by Istvan Heckenberger[3] in the years 2004–2005 by classifying arithmetic root systems and generalized Dynkin diagrams; where already Kharchenko had proven them to posess a Poincaré–Birkhoff–Witt basis of iterated (braided) commutators. The only information one requires is the braiding matrix, which is diagonal in this setting (see examples above)
While mostly only the classical Cartan-cases appear, there are several exotic diagrams possible for small primes, such as a triangle

In these cases the Weyl reflections of one diagram may not land in the "same" diagram, but a so-called Weyl equivalent. This is also the exact reason, that these exotic cases possess a Weyl-groupoid instead of a usual group (picture?).
Negative criteria: abelian subracks
Especially for irreducible V there are no submodules; however one may use the more abstract notion of subrack only reflecting the braiding of two contained elements. In several papers, Nicolas Andruskiewitsch et al. gave negative criteria excluding groups at all from possessing (indecomposable) Nichols algebras. Their techniques can be roughly summarized[10] (more details!):
- Consider a subrack that is abelian, check which representation my be inherited from the larger rack, and looked up in Heckenbegers List [3]
This ansatz puts sometimes strong conditions especially on the braiding of any g-graded element x with itself (e.g. the first example above shows q ≠ 1). Note that because g is central in the centralizer, it acts on the irreducible representation by a scalar as a consequence of the Schur lemma; hence this selfbraiding resp. 1-dim sub-Yetter-Drinfeld module / braided vectorspace / 1-dim subrack is diagonal
It is usually used to excludes g e.g. of being of odd order and/or χ of high dimension:[11]
- If g is real (i.e. conjugated to its inverse) then q = –1 (especially g has to be of even order)
- If g is quasi-real (i.e. conugated to some j-th power) then
- either q = –1 as above
- or
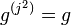 and the representation χ is one-dimensional with q = ζ3 a primitive 3rd root of unity (especially the order of g is divisible by 3)
and the representation χ is one-dimensional with q = ζ3 a primitive 3rd root of unity (especially the order of g is divisible by 3)
- If contrary g is an involution and some centralizing h = tgt then the eigenvalues of the h (viewed as matrix) acting on
![{\mathcal {O}}_{{[g]}}^{\chi }](/2014-wikipedia_en_all_02_2014/I/media/8/3/a/5/83a56ef3883c962666ac8139c3a1d669.png) is strongly restricted.
is strongly restricted.
Root systems over nonabelian groups
On the other hand, Schneider and Heckenberger established the existence an arithmetic root system over nonabelian groups[2] (as in the abelian case), including again a Weyl groupoid and a Poincaré–Birkhoff–Witt basis of iterated (braided) commutators
Immediate consequences are implied for rank 2 Nichols algebras ![{\mathfrak {B}}\left({\mathcal {O}}_{{[g]}}\oplus {\mathcal {O}}_{{[h]}}\right)](/2014-wikipedia_en_all_02_2014/I/media/5/8/5/9/58597211cb1d78864171356a31aec6f8.png) which g, h discommuting; then:
which g, h discommuting; then:
- The braided commutators [x, y] of elements
![x\in {\mathcal {O}}_{{[g]}}\;y\in {\mathcal {O}}_{{[h]}}](/2014-wikipedia_en_all_02_2014/I/media/0/a/4/1/0a414eaa39e5b35024ac92578fcf0463.png) are not all zero.
are not all zero. - The space of braided commutators
![ad_{{{\mathcal {O}}_{{[g]}}}}{\mathcal {O}}_{{[h]}}=[{\mathcal {O}}_{{[g]}},{\mathcal {O}}_{{[h]}}]](/2014-wikipedia_en_all_02_2014/I/media/7/6/d/0/76d0dedd4233324ceed16cf333af9d37.png) form an irreducible sub-Yetter–Drinfeld module
form an irreducible sub-Yetter–Drinfeld module ![{\mathcal {O}}_{{[gh]}}](/2014-wikipedia_en_all_02_2014/I/media/d/b/5/3/db539e568ec2f757cad71d8f1cd828a3.png) (i.e. the root is unique as in the Lie algebra case)
(i.e. the root is unique as in the Lie algebra case) - They're '"close to commuting"

This implies roughly, that finite dimensional Nichols algebras over nonabelian groups have to be (if at all) of very low rank.
Negative criteria: nonabelian subracks (type D)
As the abelian subracks use the structural classification of Heckenberger for Nichols algebras over abelian groups (see above) one can also consider nonabelian subracks. If such a subrack decomposes into several pieces (because now less element are present to conjugate), then the above results on root systems apply.
A specific case[11] where this is highly successful is type D, i.e. for ![r,s\in [g]\;](/2014-wikipedia_en_all_02_2014/I/media/e/8/7/4/e874e79e3acbe252a692d4a7dc04208a.png)
- r, s not conjugate in the generated subgroup

-
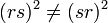
in this case the Nichols algebra of the subrack is infinite dimensional and so is the entire Nichols algebra
Known groups not admitting finite dimensional Nichols algebras
Both negation techniques above have been very fruitful to negate (indecomposable) finite-dimensional Nichols algebras:[11]
- for Alternating groupss
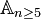 [12]
[12] - for Symmetric groups
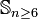 except a short list of examples[12]
except a short list of examples[12] - some group of Lie type (sources, complete list?)
- all Sporadic groups except a short list of possibilities (resp. conjugacy classes in ATLAS notation) that are all real or j = 3-quasireal:
- ...for the Fisher group
 the classes
the classes 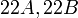
- ...for the baby monster group B the classes
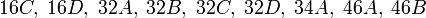
- ...for the monster group M the classes
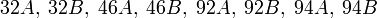
- ...for the Fisher group
Usually a large amount of conjugacy classes ae of type D ("not commutative enough"), while the others tend to posess sufficient abelian subracks and can be excluded by their consideration. Several cases have to be done by-hand. Note that the open cases tend to have very small centralizers (usually cyclic) and representations χ (usually the 1-dimensional sign representation). Significant exceptions are the conjugacy classes of order 16, 32 having as centralizers p-groups of order 2048 resp. 128 and currently no restrictions on χ.
Applications
The Nichols algebra appears as quantum Borel part in the classification of finite-dimensional pointed Hopf algebras[1] (without small primes) by Nicolas Andruskiewitsch and Hans-Jürgen Schneider, especially Quantum groups. For example 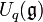 and their well known truncations for q a root of unity decompose just like an ordinary Semisimple Lie algebra into E´s (Borel part), dual F´s and K´s (Cartan algebra):
and their well known truncations for q a root of unity decompose just like an ordinary Semisimple Lie algebra into E´s (Borel part), dual F´s and K´s (Cartan algebra):
 ) spanned by the E´s, and σ (a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. See cit. loc. for an exotic example with 4 parts of type A3.
) spanned by the E´s, and σ (a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. See cit. loc. for an exotic example with 4 parts of type A3.
The classification roughly reduces a given hypothetical example to a Radford biproduct of the (coradical-) group and the (connected-) part, which contains the Nichols algebra, by taking the corresponding "graded object" (killing all linkings). With the knowledge from the classification of finite dimensional Nichols algebras above, the authors prove no additional elements to appear in the connected part (generation in degree 1), and finally describe all possible liftings as "dotted lines" in generalized Dynkin diagrams.
Recently, this correspondence has been greatly extended to identify certain so-called coideal subalgebras to be in 1:1 correspondence[13] to the Weyl group, which has been conjectued as "numercal coincidence" earlier and proven in certain cases by-hand.
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13]
- ↑ 1.0 1.1 1.2 1.3 Andruskiewitsch, Schneider: Pointed Hopf algebras, New directions in Hopf algebras, 1–68, Math. Sci. Res. Inst. Publ., 43, Cambridge Univ. Press, Cambridge, 2002.
- ↑ 2.0 2.1 2.2 2.3 Heckenberger, Schneider: Root system and Weyl gruppoid for Nichols algebras, 2008.
- ↑ 3.0 3.1 3.2 3.3 Heckenberger: Nichols algebras of diagonal type and arithmetic root systems, Habilitation thesis 2005.
- ↑ 4.0 4.1 Heckenberger: Nichols Algebras (Lecture Notes), 2008 http://www.mi.uni-koeln.de/~iheckenb/na.pdf
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Schneider, Milinski: Nichols algebras over Coxeter groups, 2000.
- ↑ 6.0 6.1 Andruskiewisch, Grana: From racks to pointed Hopf algebras, 2003.
- ↑ 7.0 7.1 Fomin,Kirilov: Quadratic algebras, Dunkl elements and Schubert calculus, 1999.
- ↑ 8.0 8.1 Grana: http://mate.dm.uba.ar/~matiasg/zoo.html
- ↑ 9.0 9.1 Heckenberger, Schneider: Nichols algebras over groups with finite root system of rank 2 I, 2010.
- ↑ 10.0 10.1 Andruskiewitsch, Fantino, Grana, Vendramin: On Nichols algebras associated to simple racks, 2010.
- ↑ 11.0 11.1 11.2 11.3 Andruskiewitsch, Fantino, Grana, Vendramin: Pointed Hopf algebras over the sporadic simple groups, 2010.
- ↑ 12.0 12.1 12.2 Andruskiewitsch, Fantino, Grana, Vendramin: Finite-dimensional pointed Hopf algebras with alternating groups are trivial, 2010.
- ↑ 13.0 13.1 Heckenberger, Schneider: Right coideal subalgebras of Nichols algebras and the Duflo order of the Weyl grupoid, 2009.
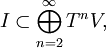
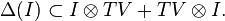
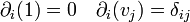
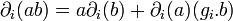
![{\mathfrak {B}}(V_{+})=k[x]\qquad {\mathfrak {B}}(V_{-})=k[x]/(x^{2})](/2014-wikipedia_en_all_02_2014/I/media/d/d/e/f/ddefb145fe4b0cdfba25eca80b22b227.png)
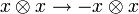
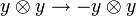
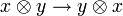

![{\mathfrak {B}}(V_{0})=k[x,y]/(x^{2},y^{2},xy+yx),](/2014-wikipedia_en_all_02_2014/I/media/5/4/f/3/54f30a76bc99db7c8d61a4bc7fdcfe3a.png)
![{\mathfrak {B}}(V_{1})=k[x]/(x^{2},y^{2},xyxy+yxyx)](/2014-wikipedia_en_all_02_2014/I/media/8/0/8/0/8080d377ebd297aae22f7ae05622683e.png)


![U_{q}({\mathfrak {g}})\cong \left({\mathfrak {B}}(V)\otimes k[{\mathbb {Z}}^{n}]\otimes {\mathfrak {B}}(V^{*})\right)^{\sigma }](/2014-wikipedia_en_all_02_2014/I/media/e/9/5/0/e9507ca8763d7a06f15ae3a7b020d30a.png)