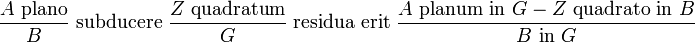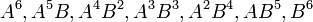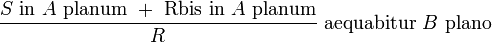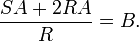New algebra

From Wikipedia, the free encyclopedia

The new algebra or symbolic analysis is a formalization of algebra promoted by François Viète in 1591 and by his successors (after 1603). It marks the beginning of the algebraic formalization (late sixteenth – the early seventeenth centuries).

The Isagoge

In artem analyticem Isagoge (1591) is the program of this large axiomatic project.

This work is available via gallica,[1] written in Latin, and announcing that it will be the first volume of a work divided into ten parts:

  • In artem Analyticem Isagoge
  • Ad Logiticem speciosam Nota priores
  • Zeteticorum libri quinque
  • De numerosa potestatum ad exegesim resolution
  • De recognitione Aequationum
  • Ad logiticem speciosam nota posteriores
  • Effectionum geometricarum Canonica recensio
  • Supllementum Geometria
  • Analytica angularium sectionum in tres partes
  • Varorium de rebus Mathematicis responsorum

It provides a new approach to writing algebra and begins with the famous dedication to the Melusinide princess Catherine de Parthenay.

Chapter I: Introduction

In the first part of his Isagoge, Viète provides definitions of his symbolic analysis, and gives, in a rhythmic movement, the definitions of Zetetic, Poristic, and Exegetic, for the purpose of writing the science of inventing Mathematics. He gives, concurrently, an axiomatic for calculation on the quantities (known and unknown) and a program, which provides heuristic rules.

  • The Zetetic is the art of translating a problem into an equation and the art of handling this equation to put it in a canonical form which gives rise to an interpretation in terms of proportions.
  • The Poristic is the examination of the truth (by the means of ordinary theorems).
  • The Exegetic, is the determination (the exhibition, says Antoine Vasset), of geometric solution or numerical solution, obtained from the general propositions of the Poristic.

In this introduction, Viète requires three steps to solve algebraic or geometrical problems: formalization, general resolution, special resolution. He adds that, contrary to the former analysts, his method will act on the resolution of symbols (non iam in numeris sed sub specie)... which is the major input. He also predicts that after his works, training in Zetetic will be done through the analysis of symbols and not by the numbers.

Chapter II About symbols, equalities, and proportions

Viète continues, in this second part, to describe the symbols and gives axiomatic rules:

  • paragraphs 1 to 6 cover the properties of equality:

Transitivity of equality, conservation sum, subtraction, product, and division

  • paragraphs 7 to 11 cover the properties of laws (addition, product, etc. with fractions).
  • paragraphs 15 and 16 explain when fractions are equal or not.

Chapter III: Des lege homogeneorum

Viète, then, continues to give the law of homogeneity, and distinguishes the symbols according to their powers, where 1 is the side (or root), 2 square, cube 3, and so on. Factors and powers are of complementary homogeneity; he notes them:

1. Length, 2 Plane, Solid 3, and 4 Plane / Plane 5 Plane / Solid 6 Solid / Solid, etc. as if he had the intuition that a geometry can be deployed beyond the ordinary dimension 3.

Chapter IV De praeceptis logistices speciosae

In this fourth chapter, Viète gives the rules of a calculus of symbols, i.e. the axioms of addition, product, etc. Symbols designate types of comparable dimension.

Firstly, his attention is focused on addition and subtraction of quantities of the same order, with rules such as A − (B + D) = A − B − D or A − (B − D) = A − B + D

Then, secondly, he defines products and quotients of homogeneous quantities. He then notes

{\frac {A{\text{ plano}}}{B}}{\text{ subducere }}{\frac {Z{\text{ quadratum}}}{G}}{\text{ residua erit }}{\frac {A{\text{ planum in }}G-Z{\text{ quadrato in }}B}{B{\text{ in }}G}}

what we note now

{\frac {A}{B}}-{\frac {Z}{G}}={\frac {AG-ZB}{BG}}

without attempting to mark the homogeneity factor.

Chapter V: Laws of the Zététic

In this chapter we have the foundations of the formulation of equations and particularly in paragraph 5 of this chapter, the idea that some letters should be reserved for known quantities (data) and other letters to unknown quantities (incertitus). Viète designates the first quantities by consonants and the others by vowels. Then, after a few propositions, the book ends with two short chapters that describe how, in practice, it is necessary to conduct the analysis of a problem, its resolution and geometrical checking.

Chapter VI: The theorems of Poristic

Chapter VII: About Rhétic (or Exegetic)

In chapter 7, on the function of the rhetic art, Viete treats the third kind of analysis (rhetic or exegetic), which is applied to numbers if the search is for a magnitude expressible in a number, as well as to lengths, planes, or solids if the thing itself must be shown, starting from canonically ordered equations.

Chapter VIII: Epilogue

In this final part Viète defines some notations, including the first and second roots (in other words square and cube roots).

Variations of 1631

The manuscript published by Vasset doesn't contain the definition of Poristic and Exegetic (ch VI and VII), but some results on the development of the binomial (to level 6) and general theorems of Poristic: which way to insert a medium proportional you want between two lengths.

This means, for instance, that the sequence

A^{6},A^{5}B,A^{4}B^{2},A^{3}B^{3},A^{2}B^{4},AB^{5},B^{6}\,

is geometric.

Reflecting Viète, Vasset writes also:

A − B cubus cubus aequabitur A cubo-cubus − 6 A quadrato-cubus in B + 15 A quad.quad. in B quad. − 20 A cubus in B cubum + 15A quadratum in B quad.-quad − 6 A B quad.-cub. + B cubus-cubus

which we denote now by:

(A-B)^{6}=A^{6}-6A^{5}B+15A^{4}B^{2}-20A^{3}B^{3}+15A^{2}B^{4}-6AB^{5}+B^{6}.\,

He then gave the rule for forming binomial coefficients (already known by Stiffel and Tartaglia), noting that he obtains the coefficients of the development, by addition in the development of the previous power, of the first and second coefficient, of the second and third, and so on.

Francois Viete

Francois Viete, French mathematician
Born 1540
Fontenay-le-Comte, Poitou
Died 23 December 1603
Paris, France
Fields algebra
Known for first notation of new algebra
Influences Ramus
Influenced Pierre de Fermat

Zététic, Poristic and Exegetic

The contributions of the new algebra

Historical critics

Viète made good Algebra with excellent geometry. However, in his desire to spend his new label under the Diophantine's aegis, Viète was taken to preserve the language of the elders. Moreover, he has no symbol to rate the multiplication, roots or equality. For example

{\frac {S{\text{ in }}A{\text{ planum }}+{\text{ Rbis in }}A{\text{ planum}}}{R}}{\text{ aequabitur }}B{\text{ plano}}

written today

{\frac {SA+2RA}{R}}=B.

Although effective, this new algebra maintained a requirement of homogeneity which is very heavy and condemns the constant reference to the meaning of geometrical parameters involved. A second Algebraic revolution will be done in the next generation with William Oughtred, Thomas Harriot, Pierre de Fermat, and finally René Descartes. Nevertheless, Viète gave us for the first time the ability to work efficiently on letters. And, for that, he must be honored as one of the fathers of Algebra.

See also

Sources

References

  1. ↑ (French) François Viète In artem analyticem Isagoge, Meteyer publisher, in Tours, (1591)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.