Nested radical
In algebra, a nested radical is a radical expression that contains another radical expression. Examples include:
which arises in discussing the regular pentagon;
or more complicated ones such as:
Denesting nested radicals
Some nested radicals can be rewritten in a form that is not nested. For example,
Rewriting a nested radical in this way is called denesting. This process is generally considered a difficult problem, although a special class of nested radical can be denested by assuming it denests into a sum of two surds:
Squaring both sides of this equation yields:
This can be solved by using the quadratic formula and setting rational and irrational parts on both sides of the equation equal to each other. The solutions for e and d can be obtained by first equating the rational parts:
which gives
For the irrational parts note that
and squaring both sides yields
By plugging in a − e for d one obtains
Rearranging terms will give an quadratic equation which can be solved for e:
The solution d is the algebraic conjugate of e. If
then
However, this approach works for nested radicals of the form
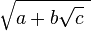 if and only if
if and only if
 is an integer, in which case the nested radical can be denested into a sum of surds.
is an integer, in which case the nested radical can be denested into a sum of surds.
In some cases, higher-power radicals may be needed to denest the nested radical.
Some identities of Ramanujan
Srinivasa Ramanujan demonstrated a number of curious identities involving denesting of radicals. Among them are the following:[1]
Other odd-looking radicals inspired by Ramanujan:
Landau's algorithm
In 1989 Susan Landau introduced the first algorithm for deciding which nested radicals can be denested.[3] Earlier algorithms worked in some cases but not others.
Infinitely nested radicals
Square roots
Under certain conditions infinitely nested square roots such as
represent rational numbers. This rational number can be found by realizing that x also appears under the radical sign, which gives the equation
If we solve this equation, we find that x = 2 (the second solution x = −1 doesn't apply, under the convention that the positive square root is meant). This approach can also be used to show that generally, if n > 0, then:
The same procedure also works to get
This method will give a rational x value for all values of n such that
Ramanujan posed this problem to the 'Journal of Indian Mathematical Society':
This can be solved by noting a more general formulation:
Setting this to F(x) and squaring both sides gives us:
Which can be simplified to:
It can then be shown that:
So, setting a =0, n = 1, and x = 2:
Ramanujan stated this radical in his lost notebook
Cube roots
In certain cases, infinitely nested cube roots such as
can represent rational numbers as well. Again, by realizing that the whole expression appears inside itself, we are left with the equation
If we solve this equation, we find that x = 2. More generally, we find that
is the real root of the equation x3 − x − n = 0 for all n > 0. For n = 1, this root is the plastic number ρ, approximately equal to 1.3247.
The same procedure also works to get
as the real root of the equation x3 + x − n = 0 for all n and x where n > 0 and |x| ≥ 1.
See also
References
- ↑ "A note on 'Zippel Denesting'", Susan Landau, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.35.5512&rep=rep1&type=pdf
- ↑ "RADICALS AND UNITS IN RAMANUJAN’S WORK", Susan Landau, http://www.math.uiuc.edu/~berndt/articles/radicals.ps
- ↑ Landau, Susan (1992). "Simplification of Nested Radicals". Journal of Computation (SIAM) 21: 85–110. doi:10.1109/SFCS.1989.63496. CiteSeerX: 10.1.1.34.2003.
Further reading
- Landau, Susan (1994). "How to Tangle with a Nested Radical". Mathematical Intelligencer 16: 49–55.
- Decreasing the Nesting Depth of Expressions Involving Square Roots
- Simplifying Square Roots of Square Roots
- Weisstein, Eric W., "Square Root", MathWorld.
- Weisstein, Eric W., "Nested Radical", MathWorld.
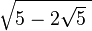
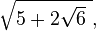
![{\sqrt[ {3}]{2+{\sqrt {3}}+{\sqrt[ {3}]{4}}\ }}.](/2014-wikipedia_en_all_02_2014/I/media/1/7/4/a/174a39bd3affcfcb3dfb0ca7aef8d78d.png)
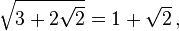
![{\sqrt[ {3}]{{\sqrt[ {3}]{2}}-1}}={\frac {1-{\sqrt[ {3}]{2}}+{\sqrt[ {3}]{4}}}{{\sqrt[ {3}]{9}}}}\,.](/2014-wikipedia_en_all_02_2014/I/media/e/3/b/6/e3b6e7d31e1d1357c066f508ec909666.png)

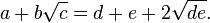
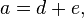

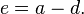
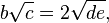
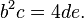

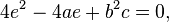
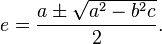
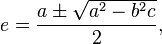

![{\sqrt[ {4}]{{\frac {3+2{\sqrt[ {4}]{5}}}{3-2{\sqrt[ {4}]{5}}}}}}={\frac {{\sqrt[ {4}]{5}}+1}{{\sqrt[ {4}]{5}}-1}}={\tfrac 12}\left(3+{\sqrt[ {4}]5}+{\sqrt 5}+{\sqrt[ {4}]{125}}\right),](/2014-wikipedia_en_all_02_2014/I/media/8/b/b/b/8bbb79c6fa2179128e2fe7a3e1a23c40.png)
![{\sqrt {{\sqrt[ {3}]{28}}-{\sqrt[ {3}]{27}}}}={\tfrac 13}\left({\sqrt[ {3}]{98}}-{\sqrt[ {3}]{28}}-1\right),](/2014-wikipedia_en_all_02_2014/I/media/e/0/c/c/e0cce988e22cd71b8ed19a6f36b201c6.png)
![{\sqrt[ {3}]{{\sqrt[ {5}]{{\frac {32}{5}}}}-{\sqrt[ {5}]{{\frac {27}{5}}}}}}={\sqrt[ {5}]{{\frac {1}{25}}}}+{\sqrt[ {5}]{{\frac {3}{25}}}}-{\sqrt[ {5}]{{\frac {9}{25}}}},](/2014-wikipedia_en_all_02_2014/I/media/8/f/a/1/8fa1d4737420fcd928dc8bd5b23744bc.png)
![{\sqrt[ {3}]{\ {\sqrt[ {3}]{2}}\ -1}}={\sqrt[ {3}]{{\frac {1}{9}}}}-{\sqrt[ {3}]{{\frac {2}{9}}}}+{\sqrt[ {3}]{{\frac {4}{9}}}}.](/2014-wikipedia_en_all_02_2014/I/media/c/e/1/f/ce1f649113a86c118571b55cbc00fa44.png)
![{\sqrt[ {4}]{49+20{\sqrt {6}}}}+{\sqrt[ {4}]{49-20{\sqrt {6}}}}=2{\sqrt {3}},](/2014-wikipedia_en_all_02_2014/I/media/e/f/4/b/ef4b270c6d7c5835ff938bd0b40be5b3.png)
![{\sqrt[ {3}]{\left({\sqrt {2}}+{\sqrt {3}}\right)\left(5-{\sqrt {6}}\right)+3\left(2{\sqrt {3}}+3{\sqrt {2}}\right)}}={\sqrt {10-{\frac {13-5{\sqrt {6}}}{5+{\sqrt {6}}}}}}.](/2014-wikipedia_en_all_02_2014/I/media/8/4/8/5/848578e0784c5a202226cef7b2e0700f.png)
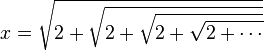
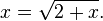
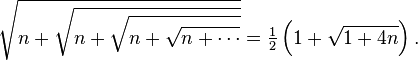
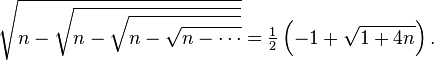
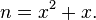
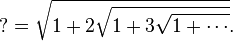


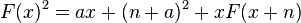
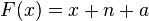
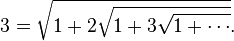

![x={\sqrt[ {3}]{6+{\sqrt[ {3}]{6+{\sqrt[ {3}]{6+{\sqrt[ {3}]{6+\cdots }}}}}}}}](/2014-wikipedia_en_all_02_2014/I/media/9/c/0/7/9c07e6f55e92bd1a2fa87f1bd41223b8.png)
![x={\sqrt[ {3}]{6+x}}.](/2014-wikipedia_en_all_02_2014/I/media/7/5/3/c/753c6e08322531eea1497949bb180bc5.png)
![{\sqrt[ {3}]{n+{\sqrt[ {3}]{n+{\sqrt[ {3}]{n+{\sqrt[ {3}]{n+\cdots }}}}}}}}](/2014-wikipedia_en_all_02_2014/I/media/a/1/4/4/a144b1b877dd246368139e373732bfa2.png)
![{\sqrt[ {3}]{n-{\sqrt[ {3}]{n-{\sqrt[ {3}]{n-{\sqrt[ {3}]{n-\cdots }}}}}}}}](/2014-wikipedia_en_all_02_2014/I/media/9/7/3/c/973c674f3ae33fd9a71349ea5a0f195d.png)