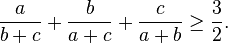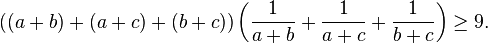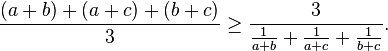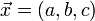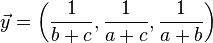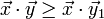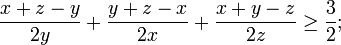Nesbitt's inequality

From Wikipedia, the free encyclopedia

In mathematics, Nesbitt's inequality is a special case of the Shapiro inequality. It states that for positive real numbers a, b and c we have:

${\frac {a}{b+c}}+{\frac {b}{a+c}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}.$

Proof

First proof

Starting from Nesbitt's inequality(1903)

${\frac {a}{b+c}}+{\frac {b}{a+c}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}$

we transform the left hand side:

${\frac {a+b+c}{b+c}}+{\frac {a+b+c}{a+c}}+{\frac {a+b+c}{a+b}}-3\geq {\frac {3}{2}}.$

Now this can be transformed into:

$((a+b)+(a+c)+(b+c))\left({\frac {1}{a+b}}+{\frac {1}{a+c}}+{\frac {1}{b+c}}\right)\geq 9.$

Division by 3 and the right factor yields:

${\frac {(a+b)+(a+c)+(b+c)}{3}}\geq {\frac {3}{{\frac {1}{a+b}}+{\frac {1}{a+c}}+{\frac {1}{b+c}}}}.$

Now on the left we have the arithmetic mean and on the right the harmonic mean, so this inequality is true.

We might also want to try to use GM for three variables.

Second proof

Suppose 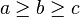$a\geq b\geq c$ , we have that

${\frac 1{b+c}}\geq {\frac 1{a+c}}\geq {\frac 1{a+b}}$

define

${\vec x}=(a,b,c)$

${\vec y}=\left({\frac 1{b+c}},{\frac 1{a+c}},{\frac 1{a+b}}\right)$

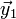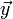The scalar product of the two sequences is maximum because of the Rearrangement inequality if they are arranged the same way, call ${\vec y}_{1}$ and ${\vec y}_{2}$ the vector ${\vec y}$ shifted by one and by two, we have:

${\vec x}\cdot {\vec y}\geq {\vec x}\cdot {\vec y}_{1}$

${\vec x}\cdot {\vec y}\geq {\vec x}\cdot {\vec y}_{2}$

Addition yields Nesbitt's inequality.

Third proof

The following identity is true for all $a,b,c:$

${\frac {a}{b+c}}+{\frac {b}{a+c}}+{\frac {c}{a+b}}={\frac {3}{2}}+{\frac {1}{2}}\left({\frac {(a-b)^{2}}{(a+c)(b+c)}}+{\frac {(a-c)^{2}}{(a+b)(b+c)}}+{\frac {(b-c)^{2}}{(a+b)(a+c)}}\right)$

This clearly proves that the left side is no less than ${\frac {3}{2}}$ for positive a,b and c.

Note: every rational inequality can be solved by transforming it to the appropriate identity, see Hilbert's seventeenth problem.

Fourth proof

Starting from Nesbitt's inequality(1903)

${\frac {a}{b+c}}+{\frac {b}{a+c}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}$

We add $3$ to both sides.

${\frac {a+b+c}{b+c}}+{\frac {a+b+c}{a+c}}+{\frac {a+b+c}{a+b}}\geq {\frac {3}{2}}+3$

Now this can be transformed into:

$(a+b+c)\left({\frac {1}{b+c}}+{\frac {1}{a+c}}+{\frac {1}{a+b}}\right)\geq {\frac {9}{2}}$

Multiply by $2$ on both sides.

$((b+c)+(a+c)+(a+b))\left({\frac {1}{b+c}}+{\frac {1}{a+c}}+{\frac {1}{a+b}}\right)\geq 9$

Which is true by the Cauchy-Schwarz inequality.

Fifth proof

Starting from Nesbitt's inequality (1903)

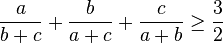${\frac {a}{b+c}}+{\frac {b}{a+c}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}$ ,

we substitute a+b=x, b+c=y, c+a=z.

Now, we get

${\frac {x+z-y}{2y}}+{\frac {y+z-x}{2x}}+{\frac {x+y-z}{2z}}\geq {\frac {3}{2}};$

this can be transformed to

${\frac {x+z}{y}}+{\frac {y+z}{x}}+{\frac {x+y}{z}}\geq {\frac {6}{1}}$

which is true, by inequality of arithmetic and geometric means.

References

Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format.

External links

See AoPS for more proofs of this inequality.
Nesbitt's inequality, PlanetMath.org.
proof of Nesbitt's inequality, PlanetMath.org.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.