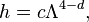Naturalness (physics)

In physics, naturalness is the property that the free parameters or physical constants appearing in a physical theory should take relative values "of order 1". That is, a natural theory would have parameters with values like 2.34 rather than 234,000 or 0.000234. This is in contrast to current theory like the standard model, where there are a number of parameters that vary by many orders of magnitude, and require extensive "fine-tuning" of those values in order for the theory to predict a universe like the one we live in.

The requirement that satisfactory theories should be "natural" in this sense is a current of thought initiated around the 1960s in particle physics. It is an aesthetic criterion, not a physical one, that arises from the seeming non-naturalness of the standard model and the broader topics of the hierarchy problem, fine-tuning, and the anthropic principle.

It is not always compatible with Occam's razor, since many instances of "natural" theories have more parameters than "fine-tuned" theories such as the Standard Model.

Introduction

In particle physics, the assumption of naturalness means that, unless a more detailed explanation exists, all conceivable terms in the effective action that preserve the required symmetries should appear in this effective action with natural coefficients.^[1]

In an effective field theory, Λ is the cutoff scale, an energy or length scale at which the theory breaks down. Due to dimensional analysis, natural coefficients have the form

where d is the dimension of the operator; and c is a dimensionless number which should be "random" and smaller than 1 at the scale where the effective theory breaks down. Further renormalization group running can reduce the value of c at an energy scale E, but by a small factor proportional to ln(E/Λ).

Some parameters in the effective action of the Standard Model seem to have far smaller coefficients than required by consistency with the assumption of naturalness, leading to some of the fundamental open questions in physics. In particular:

• The naturalness of the strong theta angle leads to the strong CP problem.
• The naturalness of the Higgs mass leads to the hierarchy problem.
• The naturalness of the cosmological constant leads to the cosmological constant problem.

In addition, the coupling of the electron to the Higgs, the mass of the electron, is abnormally small, and to a lesser extent, the masses of the light quarks.

In models with large extra dimensions, the assumption of naturalness is violated for operators which multiply field operators that create objects which are localized at different positions in the extra dimensions.^[2]

See also

• Fine tuning
• Hierarchy problem
• Large extra dimensions
• Split supersymmetry

References

1. ↑ N. Seiberg (1993). "Naturalness versus supersymmetric non-renormalization theorems". Physics Letters B 318 (3): 469–475. arXiv:hep-ph/9309335. Bibcode:1993PhLB..318..469S. doi:10.1016/0370-2693(93)91541-T. 
2. ↑ N. Arkani-Hamed, M. Schmaltz (2000). "Hierarchies without Symmetries from Extra Dimensions". Physical Review D 61 (3): 033005. arXiv:hep-ph/9903417. Bibcode:2000PhRvD..61c3005A. doi:10.1103/PhysRevD.61.033005. 

Further reading

• 't Hooft, G. (1980). "Naturalness, Chiral Symmetry and Spontaneous Chiral Symmetry Breaking". In 't Hooft, G. Recent Developments in Gauge Theories. Plenum Press. ISBN 978-0-306-40479-5. 
• Is "naturalness" unnatural? Invited talk presented at SUSY06: 14th International Conference On Supersymmetry And The Unification Of Fundamental Interactions 6/12/2006—6/17/2006
• Giudice, G. (2008). "Naturally Speaking: The Naturalness Criterion and Physics at the LHC". In Kane, G. Perspectives on LHC physics. World Scientific. ISBN 978-9812833891.