Naimark's problem

From Wikipedia, the free encyclopedia

Naimark's Problem is a question in functional analysis. It asks whether every C*-algebra that has only one $*$ up to unitary equivalence is isomorphic to the $*$ -algebra of compact operators on some (not necessarily separable) Hilbert space.

The problem has been solved in the affirmative for special cases (specifically for separable and Type-I C*-algebras). Akemann & Weaver (2004) used the 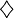$\diamondsuit$ to construct a C*-algebra with $\aleph _{{1}}$ generators that serves as a counterexample to Naimark's Problem. 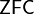More precisely, they showed that the statement "There exists a counterexample to Naimark's Problem that is generated by $\aleph _{{1}}$ elements" is independent of the axioms of Zermelo-Fraenkel Set Theory and the Axiom of Choice ( ${\mathsf {ZFC}}$ ).

External links

Akemann, Charles; Weaver, Nik (2004), "Consistency of a counterexample to Naimark's problem", Proceedings of the National Academy of Sciences of the United States of America 101 (20): 7522–7525, arXiv:math.OA/0312135, doi:10.1073/pnas.0401489101, MR 2057719

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Naimark's problem

See also

External links