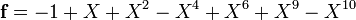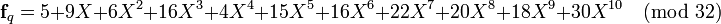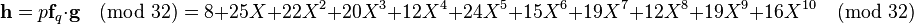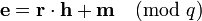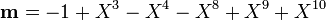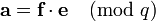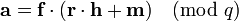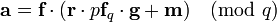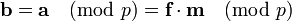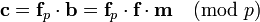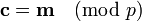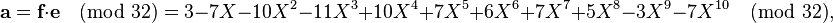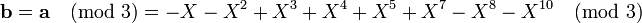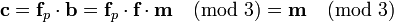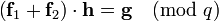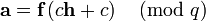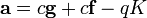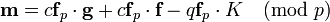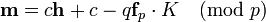NTRUEncrypt

From Wikipedia, the free encyclopedia
The NTRUEncrypt public key cryptosystem, also known as the NTRU encryption algorithm, is a lattice-based alternative to RSA and ECC and is based on the shortest vector problem in a lattice (which is not known to be breakable using quantum computers). Operations are based on objects in a truncated polynomial ring \ R=Z[X]/(X^{N}-1) with convolution multiplication and all polynomials in the ring have integer coefficients and degree at most N-1:
{\textbf {a}}=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{{N-2}}X^{{N-2}}+a_{{N-1}}X^{{N-1}}

NTRU is actually a parameterised family of cryptosystems; each system is specified by three integer parameters (N, p, q) which represent the maximal degree 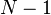\ N-1 for all polynomials in the truncated ring R, a small modulus and a large modulus, respectively, where it is assumed that N is prime, q is always larger than p, and p and q are coprime; and four sets of polynomials \ {\mathcal {L}}_{f},{\mathcal {L}}_{g},{\mathcal {L}}_{m} and \ {\mathcal {L}}_{r} (a polynomial part of the private key, a polynomial for generation of the public key, the message and a blinding value, respectively), all of degree at most \ N-1.

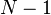It relies on the presumed difficulty of factoring certain polynomials in such rings into a quotient of two polynomials having very small coefficients. Breaking the cryptosystem is strongly related, though not equivalent, to the algorithmic problem of lattice reduction (solving the closest vector problem) in certain lattices. Careful choice of parameters is necessary to thwart some published attacks.

Since both encryption and decryption use only simple polynomial multiplication, these operations are very fast compared to other asymmetric encryption schemes, such as RSA, El Gamal and elliptic curve cryptography. However, NTRUEncrypt has not yet undergone a comparable amount of cryptographic analysis.

A related algorithm is the NTRUSign digital signature algorithm.

History

The NTRUEncrypt Public Key Cryptosystem is a relatively new cryptosystem. The first version of the system, which was simply called NTRU, was developed around 1996 by three mathematicians (J. Hoffstein, J.Pipher and J.H. Silverman). In 1996 these mathematicians together with D. Lieman founded the NTRU Cryptosystems, Inc. and were given a patent on the cryptosystem.

At first the cryptosystem sometimes failed to decrypt a message back to the original message even though the message was encrypted correctly. Even though the system sometimes failed to decrypt, the developers considered it a public key cryptosystem and thereby based their security claims on the assumption that this system was a public key cryptosystem.

During the last ten years people have been working on improving the cryptosystem. Since the first presentation of the cryptosystem, some changes were made to improve both the performance of the system and its security. Most performance improvements were focussed on speeding up the process, rather than fixing the problem of incorrect decryption. Up till 2005 literature can be found that describes the decryption failures of the NTRUEncrypt. As for security, since the first version of the NTRUEncrypt, new parameters have been introduced that seem secure for all currently known attacks and reasonable increase in computation power. Now the system is fully accepted to IEEE P1363 standards under the specifications for lattice-based public-key cryptography (IEEE P1363.1). Because of the speed of the NTRUEncrypt Public Key Cryptosystem (see http://bench.cr.yp.to for benchmarking results) and its low memory use (see below), it can be used in applications such as mobile devices and Smart-cards. In April 2011, NTRUEncrypt was accepted as a X9.98 Standard, for use in the financial services industry.[1]

Public key generation

Sending a secret message from Alice to Bob requires the generation of a public and a private key. The public key is known by both Alice and Bob and the private key is only known by Bob. To generate the key pair two polynomials f and g, with coefficients much smaller than q, with degree at most 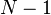\ N-1 and with coefficients in {-1,0,1} are required. They can be considered as representations of the residue classes of polynomials modulo \ X^{N}-1 in R. 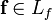The polynomial {\textbf {f}}\in L_{f} must satisfy the additional requirement that the inverses modulo q and modulo p (computed using the Euclidean algorithm) exist, which means that 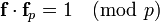\ {\textbf {f}}\cdot {\textbf {f}}_{p}=1{\pmod p} and \ {\textbf {f}}\cdot {\textbf {f}}_{q}=1{\pmod q} must hold. So when the chosen f is not invertible, Bob has to go back and try another f.

Both f and \ {\mathbf {f}}_{p} are Bob’s private key. The public key h is generated computing the quantity

{\textbf {h}}=p{\textbf {f}}_{q}\cdot {\textbf {g}}{\pmod q}.

Example: In this example the parameters (N, p, q) will have the values N = 11, p = 3 and q = 32 and therefore the polynomials f and g are of degree at most 10. The system parameters (N, p, q) are known to everybody. The polynomials are randomly chosen, so suppose they are represented by

{\textbf {f}}=-1+X+X^{2}-X^{4}+X^{6}+X^{9}-X^{{10}}
{\textbf {g}}=-1+X^{2}+X^{3}+X^{5}-X^{8}-X^{{10}}

Using the Euclidean algorithm the inverse of f modulo p and modulo q, respectively, is computed

{\textbf {f}}_{p}=1+2X+2X^{3}+2X^{4}+X^{5}+2X^{7}+X^{8}+2X^{9}{\pmod 3}
{\textbf {f}}_{q}=5+9X+6X^{2}+16X^{3}+4X^{4}+15X^{5}+16X^{6}+22X^{7}+20X^{8}+18X^{9}+30X^{{10}}{\pmod {32}}

Which creates the public key h (known to both Alice and Bob) computing the product

{\textbf {h}}=p{\textbf {f}}_{q}\cdot {\textbf {g}}{\pmod {32}}=8+25X+22X^{2}+20X^{3}+12X^{4}+24X^{5}+15X^{6}+19X^{7}+12X^{8}+19X^{9}+16X^{{10}}{\pmod {32}}

Encryption

Alice, who wants to send a secret message to Bob, puts her message in the form of a polynomial m with coefficients {-1,0,1}. In modern applications of the encryption, the message polynomial can be translated in a binary or ternary representation. After creating the message polynomial, Alice chooses randomly a polynomial r with small coefficients (not restricted to the set {-1,0,1}), that is meant to obscure the message.

With Bob’s public key h the encrypted message e is computed:

{\textbf {e}}={\textbf {r}}\cdot {\textbf {h}}+{\textbf {m}}{\pmod q}

This ciphertext hides Alice’s messages and can be sent safely to Bob.

Example: Assume that Alice wants to send a message that can be written as polynomial

{\textbf {m}}=-1+X^{3}-X^{4}-X^{8}+X^{9}+X^{{10}}

and that the randomly chosen ‘blinding value’ can be expressed as

{\textbf {r}}=-1+X^{2}+X^{3}+X^{4}-X^{5}-X^{7}

The ciphertext e that represents her encrypted message to Bob will look like

{\textbf {e}}={\textbf {r}}\cdot {\textbf {h}}+{\textbf {m}}{\pmod {32}}=14+11X+26X^{2}+24X^{3}+14X^{4}+16X^{5}+30X^{6}+7X^{7}+25X^{8}+6X^{9}+19X^{{10}}{\pmod {32}}

Decryption

Anybody knowing r could compute the message m; so r must not be revealed by Alice. In addition to the publicly available information, Bob knows his own private key. Here is how he can obtain m: First he multiplies the encrypted message e and part of his private key f

{\textbf {a}}={\textbf {f}}\cdot {\textbf {e}}{\pmod q}

By rewriting the polynomials, this equation is actually representing the following computation:

{\textbf {a}}={\textbf {f}}\cdot {\textbf {e}}{\pmod q}
{\textbf {a}}={\textbf {f}}\cdot ({\textbf {r}}\cdot {\textbf {h}}+{\textbf {m}}){\pmod q}
{\textbf {a}}={\textbf {f}}\cdot ({\textbf {r}}\cdot p{\textbf {f}}_{q}\cdot {\textbf {g}}+{\textbf {m}}){\pmod q}
{\textbf {a}}=p{\textbf {r}}\cdot {\textbf {g}}+{\textbf {f}}\cdot {\textbf {m}}{\pmod q}

Instead of choosing the coefficients of a between 0 and q – 1 they are chosen in the interval [-q/2, q/2] to prevent that the original message may not be properly recovered since Alice chooses the coordinates of her message m in the interval [-p/2, p/2]. This implies that all coefficients of 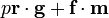\ p{\textbf {r}}\cdot {\textbf {g}}+{\textbf {f}}\cdot {\textbf {m}} already lie within the interval [-q/2, q/2] because the polynomials r, g, f and m and prime p all have coefficients that are small compared to q. This means that all coefficients are left unchanged during reducing modulo q and that the original message may be recovered properly.

The next step will be to calculate a modulo p:

{\textbf {b}}={\textbf {a}}{\pmod p}={\textbf {f}}\cdot {\textbf {m}}{\pmod p}

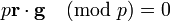because \ p{\textbf {r}}\cdot {\textbf {g}}{\pmod p}=0.

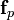
Knowing b Bob can use the other part of his private key \ \left({\textbf {f}}_{p}\right) to recover Alice’s message by multiplication of b and \ {\textbf {f}}_{p}

{\textbf {c}}={\textbf {f}}_{p}\cdot {\textbf {b}}={\textbf {f}}_{p}\cdot {\textbf {f}}\cdot {\textbf {m}}{\pmod p}
{\textbf {c}}={\textbf {m}}{\pmod p}

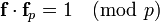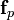because the property \ {\textbf {f}}\cdot {\textbf {f}}_{p}=1{\pmod p} was required for \ {\textbf {f}}_{p}.

Example: The encrypted message e from Alice to Bob is multiplied with polynomial f

{\textbf {a}}={\textbf {f}}\cdot {\textbf {e}}{\pmod {32}}=3-7X-10X^{2}-11X^{3}+10X^{4}+7X^{5}+6X^{6}+7X^{7}+5X^{8}-3X^{9}-7X^{{10}}{\pmod {32}},

where Bob uses the interval [-q/2, q/2] instead of the interval [0, q – 1] for the coefficients of polynomial a to prevent that the original message may not be recovered correctly.

Reducing the coefficients of a mod p results in

{\textbf {b}}={\textbf {a}}{\pmod 3}=-X-X^{2}+X^{3}+X^{4}+X^{5}+X^{7}-X^{8}-X^{{10}}{\pmod 3}

which equals 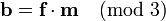\ {\textbf {b}}={\textbf {f}}\cdot {\textbf {m}}{\pmod 3}.

In the last step the result is multiplied with 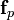\ {\textbf {f}}_{p} from Bob’s private key to end up with the original message m

{\textbf {c}}={\textbf {f}}_{p}\cdot {\textbf {b}}={\textbf {f}}_{p}\cdot {\textbf {f}}\cdot {\textbf {m}}{\pmod 3}={\textbf {m}}{\pmod 3}
{\textbf {c}}=-1+X^{3}-X^{4}-X^{8}+X^{9}+X^{{10}}

Which indeed is the original message Alice has sent to Bob!

Attacks

Since the proposal of NTRU several attacks on the NTRUEncrypt public key cryptosystem have been introduced. Most attacks are focused on making a total break by finding the secret key f instead of just recovering the message m. If f is known to have very few non-zero coefficients Eve can successfully mount a brute force attack by trying all values for f. When Eve wants to know whether f´ is the secret key, she simply calculates 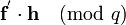\ {\textbf {f}}^{{'}}\cdot {\textbf {h}}{\pmod q}. If it has small coefficients it might be the secret key f, and Eve can test if f´ is the secret key by using it to decrypt a message she encrypted herself. 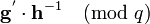Eve could also try values of g and test if \ {\textbf {g}}^{{'}}\cdot {\textbf {h}}^{{-1}}{\pmod q}has small values.

It is possible to mount a meet-in-the-middle attack which is more powerful. It can cut the search time by square root. The attack is based on the property that \ {\textbf {f}}\cdot {\textbf {h}}={\textbf {g}}{\pmod q}.

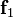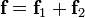Eve wants to find \ {\textbf {f}}_{1} and \ {\textbf {f}}_{2} such that \ {\textbf {f}}={\textbf {f}}_{1}+{\textbf {f}}_{2} holds and such that they have the property

\left({\textbf {f}}_{1}+{\textbf {f}}_{2}\right)\cdot {\textbf {h}}={\textbf {g}}{\pmod q}
{\textbf {f}}_{1}\cdot {\textbf {h}}={\textbf {g}}-{\textbf {f}}_{2}\cdot {\textbf {h}}{\pmod q}

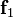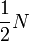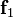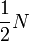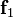If f has d one’s and N-d zero’s, then Eve creates all possible \ {\textbf {f}}_{1} and \ {\textbf {f}}_{2} in which they both have length \ {\frac {1}{2}}N (e.g. \ {\textbf {f}}_{1} covers the \ {\frac {1}{2}}N lowest coefficients of f and \ {\textbf {f}}_{2} the highest) with d/2 one’s. Then she computes {\textbf {f}}_{1}\cdot {\textbf {h}}{\pmod q} for all \ {\textbf {f}}_{1} and orders them in bins based on the first k coordinates. After that she computes all 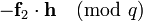\ -{\textbf {f}}_{2}\cdot {\textbf {h}}{\pmod q} and orders them in bins not only based on the first k coordinates, but also based on what happens if you add 1 to the first k coordinates. 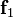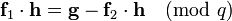Then you check the bins that contain both \ {\textbf {f}}_{1} and \ {\textbf {f}}_{2} and see if the property \ {\textbf {f}}_{1}\cdot {\textbf {h}}={\textbf {g}}-{\textbf {f}}_{2}\cdot {\textbf {h}}{\pmod q} holds.

The lattice reduction attack is one of the best known and one of the most practical methods to break the NTRUEncrypt. In a way it can be compared to the factorization of the modulus in RSA. The most used algorithm for the lattice reduction attack is the Lenstra-Lenstra-Lovàsz algorithm. Because the public key h contains both f and g one can try to obtain them from h. It is however too hard to find the secret key when the NTRUEncrypt parameters are chosen secure enough. The lattice reduction attack becomes harder if the dimension of the lattice gets bigger and the shortest vector gets longer.

The chosen ciphertext attack is also a method which recovers the secret key f and thereby results in a total break. In this attack Eve tries to obtain her own message from the ciphertext and thereby tries to obtain the secret key. In this attack Eve doesn’t have any interaction with Bob.

How it works:

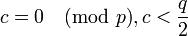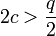First Eve creates a cipher text \ {\textbf {e}}=c{\textbf {h}}+c such that \ c=0{\pmod p},c<{\frac {q}{2}} and \ 2c>{\frac {q}{2}} When Eve writes down the steps to deciphers e (without actually calculating the values since she does not know f) she finds \ {\textbf {a}}={\textbf {f}}\cdot {\textbf {e}}{\pmod q}:

{\textbf {a}}={\textbf {f}}\left(c{\textbf {h}}+c\right){\pmod q}
{\textbf {a}}=c{\textbf {g}}+c{\textbf {f}}{\pmod q}
{\textbf {a}}=c{\textbf {g}}+c{\textbf {f}}-qK

In which \ K=\sum k_{i}x^{i} such that

k_{i}={\begin{cases}1\ \ \qquad {\text{if the}}\ i^{{th}}\ {\text{coefficient of}}\ {\textbf {f}}\ {\text{and}}\ {\textbf {g}}\ {\text{is}}\ 1\\-1\qquad {\text{if the}}\ i^{{th}}\ {\text{coefficient of}}\ {\textbf {f}}\ {\text{and}}\ {\textbf {g}}\ {\text{is}}\ -1\\0\ \ \qquad {\text{Otherwise}}\end{cases}}

Example:

{\textbf {f}}=-1+X+X^{2}-X^{4}+X^{6}+X^{9}-X^{{10}}
{\textbf {g}}=-1+X^{2}+X^{3}+X^{5}-X^{8}-X^{{10}}

Then K becomes 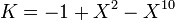\ K=-1+X^{2}-X^{{10}}.

Reducing the coefficients of polynomials a mod p really reduces the coefficients of 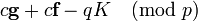\ c{\textbf {g}}+c{\textbf {f}}-qK{\pmod p}. After multiplication with 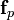\ {\textbf {f}}_{p}, Eve finds:

{\textbf {m}}=c{\textbf {f}}_{p}\cdot {\textbf {g}}+c{\textbf {f}}_{p}\cdot {\textbf {f}}-q{\textbf {f}}_{p}\cdot K{\pmod p}
{\textbf {m}}=c{\textbf {h}}+c-q{\textbf {f}}_{p}\cdot K{\pmod p}

Because c was chosen to be a multiple of p, m can be written as

{\textbf {m}}=-q{\textbf {f}}_{p}\cdot K{\pmod p}

Which means that 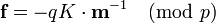\ {\textbf {f}}=-qK\cdot {\textbf {m}}^{{-1}}{\pmod p}.

Now if f and g have few coefficients which are the same at the same factors, K has few non zero coefficients and is thereby small. By trying different values of K the attacker can recover f.

By encrypting and decrypting a message according to the NTRUEncrypt the attacker can check whether the function f is the correct secret key or not.

Security and performance improvements

Using the latest suggested parameters (see below) the NTRUEncrypt public key cryptosystem is secure to most attacks. There continues however to be a struggle between performance and security. It is hard to improve the security without slowing down the speed, and vice versa.

One way to speed up the process without damaging the effectiveness of the algorithm, is to make some changes in the secret key f. First, construct f such that 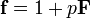\ {\textbf {f}}=1+p{\textbf {F}}, in which F is a small polynomial (i.e. coefficients {-1,0, 1}). By constructing f this way, f is invertible mod p. In fact \ {\textbf {f}}^{{-1}}=1{\pmod p}, which means that Bob does not have to actually calculate the inverse and that Bob does not have to conduct the second step of decryption. 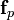Therefore constructing f this way saves a lot of time but it does not affect the security of the NTRUEncrypt because it is only easier to find \ {\textbf {f}}_{p} but f is still hard to recover. In this case f has coefficients different from -1, 0 or 1, because of the multiplication by p. But because Bob multiplies by p to generate the public key h, and later on reduces the ciphertext modulo p, this will not have an effect on the encryption method.

Second, f can be written as the product of multiple polynomials, such that the polynomials have many zero coefficients. This way fewer calculations have to be conducted.

In most commercial applications of the NTRUEncrypt, the parameter N=251 is used. To avoid lattice attacks, brute force attacks and meet-in-the-middle attacks, f and g should have about 72 non-zero coefficients.

According to the latest research [2] the following parameters are considered secure:

Table 1: Parameters

N q p
Moderate Security 167 128 3
Standard Security 251 128 3
High Security 347 128 3
Highest Security 503 256 3

References

  1. ↑ http://www.businesswire.com/news/home/20110411005309/en/Security-Innovation%E2%80%99s-NTRUEncrypt-Adopted-X9-Standard-Data
  2. ↑ NTRU PKCS Parameters
  • Jaulmes, E. and Joux, A. A Chosen-Ciphertext Attack against NTRU. Lecture notes in computer science; Vol 1880. Proceedings of the 20th Annual International Cryptology Conference on Advances in Cryptography. pp. 20–35, 2000.
  • Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman. NTRU: A Ring Based Public Key Cryptosystem. In Algorithmic Number Theory (ANTS III), Portland, OR, June 1998, J.P. Buhler (ed.), Lecture Notes in Computer Science 1423, Springer-Verlag, Berlin, 1998, 267-288.
  • Howgrave-Graham, N., Silverman, J.H. & Whyte, W., Meet-In-The-Middle Attack on a NTRU Private Key.
  • J. Hoffstein, J. Silverman. Optimizations for NTRU. Public-Key Cryptography and Computational Number Theory (Warsaw, September 11–15, 2000), DeGruyter, to appear.
  • A. C. Atici, L. Batina, J. Fan & I. Verbauwhede. Low-cost implementations of NTRU for pervasive security.

External links

 
Algorithms
Theory
Standardization
Topics
 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.