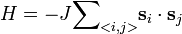N-vector model

From Wikipedia, the free encyclopedia

The n-vector model or O(n) model is one of the many highly simplified models in the branch of physics known as statistical mechanics. In the n-vector model, n-component, unit length, classical spins ${\mathbf {s}}_{i}$ are placed on the vertices of a lattice. The Hamiltonian of the n-vector model is given by:

$H=-J{\sum }_{{<i,j>}}{\mathbf {s}}_{i}\cdot {\mathbf {s}}_{j}$

where the sum runs over all pairs of neighboring spins $<i,j>$ and $\cdot$ denotes the standard Euclidean inner product. Special cases of the n-vector model are:

$n=0$ || The Self-Avoiding Walks (SAW)

$n=1$ || The Ising model

$n=2$ || The XY model

$n=3$ || The Heisenberg model

$n=4$ || Toy model for the Higgs sector of the Standard Model

The general mathematical formalism used to describe and solve the n-vector model and certain generalizations are developed in the article on the Potts model.

References

P.G. de Gennes, Phys. Lett. A, 38, 339 (1972) noticed that the $n=0$ case corresponds to the SAW.
George Gaspari, Joseph Rudnick, Phys. Rev. B, 33, 3295 (1986) discuss the model in the limit of $n$ going to 0.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.