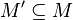Multi-track Turing machine

From Wikipedia, the free encyclopedia

Turing machines
Machine
Universal Turing machine Alternating Turing machine Quantum Turing machine Non-deterministic Turing machine Read-only Turing machine Read-only right moving Turing machines Probabilistic Turing machine Multi-track Turing machine Turing machine equivalents Turing machine examples
Science
Alan Turing Category:Turing machine
v t e

A Multitrack Turing machine is a specific type of Multi-tape Turing machine. In a standard n-tape Turing machine, n heads move independently along n tracks. In a n-track Turing machine, one head reads and writes on all tracks simultaneously. A tape position in a n-track Turing Machine contains n symbols from the tape alphabet. It is equivalent to the standard Turing machine and therefore accepts precisely the recursively enumerable languages.

Formal definition

A multitape Turing machine can be formally defined as a 6-tuple $M=\langle Q,\Sigma ,\Gamma ,\delta ,q_{0},F\rangle$ , where

$Q$ is a finite set of states
$\Sigma$ is a finite set of symbols called the tape alphabet
$\Gamma \in Q$
$q_{0}\in Q$ is the initial state
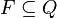$F\subseteq Q$ is the set of final or accepting states.
$\delta \subseteq \left(Q\backslash A\times \Sigma \right)\times \left(Q\times \Sigma \times d\right)$ is a relation on states and symbols called the transition relation.
$\delta \left(Q_{i},[x_{1},x_{2}...x_{n}]\right)=(Q_{j},[y_{1},y_{2}...y_{n}],d)$

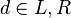
where $d\in {L,R}$

Proof of equivalency to standard Turing machine

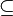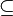This will prove that a two-track Turing machine is equivalent to a standard Turing machine. This can be generalized to a n-track Turing machine. Let L be a recursively enumerable language. Let M= $\langle Q,\Sigma ,\Gamma ,\delta ,q_{0},F\rangle$ be standard Turing machine that accepts L. Let M' is a two-track Turing machine. To prove M=M' it must be shown that M $\subseteq$ M' and M' $\subseteq$ M

$M\subseteq M'$

If all but the first track is ignored then M and M' are clearly equivalent.

$M'\subseteq M$

The tape alphabet of a one-track Turing machine equivalent to a two-track Turing machine consists of an ordered pair. The input symbol a of a Turing machine M' can be identified as an ordered pair [x,y] of Turing machine M. The one-track Turing machine is:

M= $\langle Q,\Sigma \times {B},\Gamma \times \Gamma ,\delta ',q_{0},F\rangle$ with the transition function $\delta \left(q_{i},[x_{1},x_{2}]\right)=\delta '\left(q_{i},[x_{1},x_{2}]\right)$

This machine also accepts L.

References

Thomas A. Sudkamp (2006). Languages and Machines, Third edition. Adison Wesley. ISBN 0-321-32221-5. Chapter 8.6: Multitape Machines: pp 269-271

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.