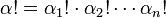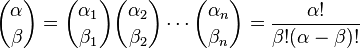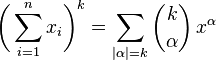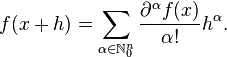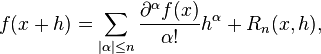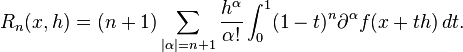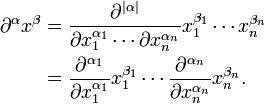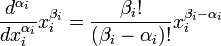Multi-index notation

From Wikipedia, the free encyclopedia

Calculus
Fundamental theorem Limits of functions Continuity Mean value theorem Rolle's theorem
Differential calculus Definitions Derivative Differential (infinitesimal) Differential of a function Generalizations of the derivative Concepts Notation for differentiation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem Rules and identities Sums Products Chain rule Powers Quotients Faà di Bruno's formula
Integral calculus Lists of integrals Definitions Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral Integration by parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series Geometric Arithmetico-geometric Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (Term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector calculus Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem Directional derivative
Multivariable calculus Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian
Specialized calculi Calculus of variations Fractional Malliavin Stochastic
v t e

The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices.

Multi-index notation

An n-dimensional multi-index is an n-tuple

$\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$

of non-negative integers (i.e. an element of the n-dimensional set of natural numbers, denoted ${\mathbb {N}}_{0}^{n}$ ).

For multi-indices $\alpha ,\beta \in {\mathbb {N}}_{0}^{n}$ and $x=(x_{1},x_{2},\ldots ,x_{n})\in {\mathbb {R}}^{n}$ one defines:

Componentwise sum and difference: $\alpha \pm \beta =(\alpha _{1}\pm \beta _{1},\,\alpha _{2}\pm \beta _{2},\ldots ,\,\alpha _{n}\pm \beta _{n})$

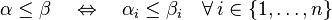
Partial order: $\alpha \leq \beta \quad \Leftrightarrow \quad \alpha _{i}\leq \beta _{i}\quad \forall \,i\in \{1,\ldots ,n\}$

Sum of components (absolute value): $|\alpha |=\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}$

Factorial: $\alpha !=\alpha _{1}!\cdot \alpha _{2}!\cdots \alpha _{n}!$

Binomial coefficient: ${\binom {\alpha }{\beta }}={\binom {\alpha _{1}}{\beta _{1}}}{\binom {\alpha _{2}}{\beta _{2}}}\cdots {\binom {\alpha _{n}}{\beta _{n}}}={\frac {\alpha !}{\beta !(\alpha -\beta )!}}$

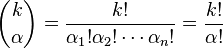
Multinomial coefficient: ${\binom {k}{\alpha }}={\frac {k!}{\alpha _{1}!\alpha _{2}!\cdots \alpha _{n}!}}={\frac {k!}{\alpha !}}$

where $k:=|\alpha |\in {\mathbb {N}}_{0}\,\!$ .

Power: $x^{\alpha }=x_{1}^{{\alpha _{1}}}x_{2}^{{\alpha _{2}}}\ldots x_{n}^{{\alpha _{n}}}$ .

Higher-order partial derivative

$\partial ^{\alpha }=\partial _{1}^{{\alpha _{1}}}\partial _{2}^{{\alpha _{2}}}\ldots \partial _{n}^{{\alpha _{n}}}$

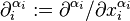where $\partial _{i}^{{\alpha _{i}}}:=\partial ^{{\alpha _{i}}}/\partial x_{i}^{{\alpha _{i}}}$ (see also 4-gradient).

Some applications

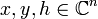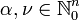The multi-index notation allows the extension of many formulae from elementary calculus to the corresponding multi-variable case. Below are some examples. In all the following, $x,y,h\in {\mathbb {C}}^{n}$ (or ${\mathbb {R}}^{n}$ ), $\alpha ,\nu \in {\mathbb {N}}_{0}^{n}$ , and $f,a_{\alpha }\colon {\mathbb {C}}^{n}\to {\mathbb {C}}$ (or ${\mathbb {R}}^{n}\to {\mathbb {R}}$ ).

Multinomial theorem

${\biggl (}\sum _{{i=1}}^{n}x_{i}{\biggr )}^{k}=\sum _{{|\alpha |=k}}{\binom {k}{\alpha }}\,x^{\alpha }$

Multi-binomial theorem

$(x+y)^{\alpha }=\sum _{{\nu \leq \alpha }}{\binom {\alpha }{\nu }}\,x^{\nu }y^{{\alpha -\nu }}.$

Note that, since $x + y$ is a vector and $α$ is a multi-index, the expression on the left is short for $(x 1 + y 1) α 1 ...(x n + y n) α n$ .

Leibniz formula

For smooth functions f and g

$\partial ^{\alpha }(fg)=\sum _{{\nu \leq \alpha }}{\binom {\alpha }{\nu }}\,\partial ^{{\nu }}f\,\partial ^{{\alpha -\nu }}g.$

Taylor series

For an analytic function f in n variables one has

$f(x+h)=\sum _{{\alpha \in {\mathbb {N}}_{0}^{n}}}^{{}}{{\frac {\partial ^{{\alpha }}f(x)}{\alpha !}}h^{\alpha }}.$

In fact, for a smooth enough function, we have the similar Taylor expansion

$f(x+h)=\sum _{{|\alpha |\leq n}}{{\frac {\partial ^{{\alpha }}f(x)}{\alpha !}}h^{\alpha }}+R_{{n}}(x,h),$

where the last term (the remainder) depends on the exact version of Taylor's formula. For instance, for the Cauchy formula (with integral remainder), one gets

$R_{n}(x,h)=(n+1)\sum _{{|\alpha |=n+1}}{\frac {h^{\alpha }}{\alpha !}}\int _{0}^{1}(1-t)^{n}\partial ^{\alpha }f(x+th)\,dt.$

General partial differential operator

A formal N-th order partial differential operator in n variables is written as

$P(\partial )=\sum _{{|\alpha |\leq N}}{}{a_{{\alpha }}(x)\partial ^{{\alpha }}}.$

Integration by parts

For smooth functions with compact support in a bounded domain 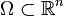$\Omega \subset {\mathbb {R}}^{n}$ one has

$\int _{{\Omega }}{}{u(\partial ^{{\alpha }}v)}\,dx=(-1)^{{|\alpha |}}\int _{{\Omega }}^{{}}{(\partial ^{{\alpha }}u)v\,dx}.$

This formula is used for the definition of distributions and weak derivatives.

An example theorem

If $\alpha ,\beta \in {\mathbb {N}}_{0}^{n}$ are multi-indices and 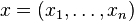$x=(x_{1},\ldots ,x_{n})$ , then

$\partial ^{\alpha }x^{\beta }={\begin{cases}{\frac {\beta !}{(\beta -\alpha )!}}x^{{\beta -\alpha }}&{\hbox{if}}\,\,\alpha \leq \beta ,\\0&{\hbox{otherwise.}}\end{cases}}$

Proof

The proof follows from the power rule for the ordinary derivative; if α and β are in {0, 1, 2, . . .}, then

${\frac {d^{\alpha }}{dx^{\alpha }}}x^{\beta }={\begin{cases}{\frac {\beta !}{(\beta -\alpha )!}}x^{{\beta -\alpha }}&{\hbox{if}}\,\,\alpha \leq \beta ,\\0&{\hbox{otherwise.}}\end{cases}}\qquad (1)$

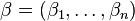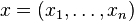Suppose $\alpha =(\alpha _{1},\ldots ,\alpha _{n})$ , $\beta =(\beta _{1},\ldots ,\beta _{n})$ , and $x=(x_{1},\ldots ,x_{n})$ . Then we have that

${\begin{aligned}\partial ^{\alpha }x^{\beta }&={\frac {\partial ^{{\vert \alpha \vert }}}{\partial x_{1}^{{\alpha _{1}}}\cdots \partial x_{n}^{{\alpha _{n}}}}}x_{1}^{{\beta _{1}}}\cdots x_{n}^{{\beta _{n}}}\\&={\frac {\partial ^{{\alpha _{1}}}}{\partial x_{1}^{{\alpha _{1}}}}}x_{1}^{{\beta _{1}}}\cdots {\frac {\partial ^{{\alpha _{n}}}}{\partial x_{n}^{{\alpha _{n}}}}}x_{n}^{{\beta _{n}}}.\end{aligned}}$

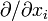For each i in {1, . . ., n}, the function $x_{i}^{{\beta _{i}}}$ only depends on $x_{i}$ . In the above, each partial differentiation $\partial /\partial x_{i}$ therefore reduces to the corresponding ordinary differentiation $d/dx_{i}$ . Hence, from equation (1), it follows that $\partial ^{\alpha }x^{\beta }$ vanishes if α_i > β_i for at least one i in {1, . . ., n}. If this is not the case, i.e., if α ≤ β as multi-indices, then

${\frac {d^{{\alpha _{i}}}}{dx_{i}^{{\alpha _{i}}}}}x_{i}^{{\beta _{i}}}={\frac {\beta _{i}!}{(\beta _{i}-\alpha _{i})!}}x_{i}^{{\beta _{i}-\alpha _{i}}}$

for each $i$ and the theorem follows. $\Box$

References

Saint Raymond, Xavier (1991). Elementary Introduction to the Theory of Pseudodifferential Operators. Chap 1.1 . CRC Press. ISBN 0-8493-7158-9

This article incorporates material from multi-index derivative of a power on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Multi-index notation