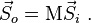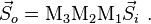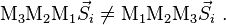Mueller calculus

From Wikipedia, the free encyclopedia

Mueller calculus is a matrix method for manipulating Stokes vectors, which represent the polarization of light. It was developed in 1943 by Hans Mueller, a professor of physics at the Massachusetts Institute of Technology. In this technique, the effect of a particular optical element is represented by a Mueller matrix—a 4×4 matrix that is a generalization of the Jones matrix.

Light which is unpolarized or partially polarized must be treated using Mueller calculus, while fully polarized light can be treated with either Mueller calculus or the simpler Jones calculus. Many problems involving coherent light (such as from a laser) must be treated with Jones calculus, because it works with amplitude rather than intensity of light, and retains information about the phase of the waves.

Any fully polarized, partially polarized, or unpolarized state of light can be represented by a Stokes vector (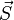 ${\vec S}$ ). Any optical element can be represented by a Mueller matrix (M).

If a beam of light is initially in the state 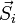${\vec S}_{i}$ and then passes through an optical element M and comes out in a state 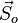${\vec S}_{o}$ , then it is written

${\vec S}_{o}={\mathrm M}{\vec S}_{i}\ .$

If a beam of light passes through optical element M₁ followed by M₂ then M₃ it is written

${\vec S}_{o}={\mathrm M}_{3}{\big (}{\mathrm M}_{2}({\mathrm M}_{1}{\vec S}_{i}){\big )}\$

given that matrix multiplication is associative it can be written

${\vec S}_{o}={\mathrm M}_{3}{\mathrm M}_{2}{\mathrm M}_{1}{\vec S}_{i}\ .$

Matrix multiplication is not commutative, so in general

${\mathrm M}_{3}{\mathrm M}_{2}{\mathrm M}_{1}{\vec S}_{i}\neq {\mathrm M}_{1}{\mathrm M}_{2}{\mathrm M}_{3}{\vec S}_{i}\ .$

Below are listed the Mueller matrices for some ideal common optical elements:

${1 \over 2}{\begin{pmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}\quad$ Linear polarizer (Horizontal Transmission)

${1 \over 2}{\begin{pmatrix}1&-1&0&0\\-1&1&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}\quad$ Linear polarizer (Vertical Transmission)

${1 \over 2}{\begin{pmatrix}1&0&1&0\\0&0&0&0\\1&0&1&0\\0&0&0&0\end{pmatrix}}\quad$ Linear polarizer (+45° Transmission)

${1 \over 2}{\begin{pmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\end{pmatrix}}\quad$ Linear polarizer (-45° Transmission)

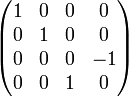${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&-1\\0&0&1&0\end{pmatrix}}\quad$ Quarter wave plate (fast-axis vertical)

${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&-1&0\end{pmatrix}}\quad$ Quarter wave plate (fast-axis horizontal)

${\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}\quad$ Half wave plate (fast-axis vertical)

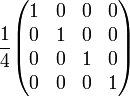${1 \over 4}{\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}\quad$ Attenuating filter (25% Transmission)

References

E. Collett, Field Guide to Polarization, SPIE Field Guides vol. FG05, SPIE (2005). ISBN 0-8194-5868-6.
E. Hecht, Optics, 2nd ed., Addison-Wesley (1987). ISBN 0-201-11609-X.
del Toro Iniesta, Jose Carlos (2003). Introduction to Spectropolarimetry. Cambridge, UK: Cambridge University Press. p. 227. ISBN 978-0-521-81827-8.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Mueller calculus

See also

References