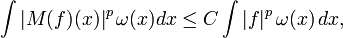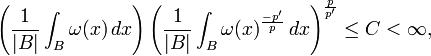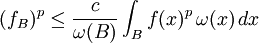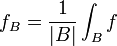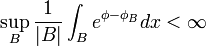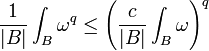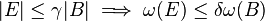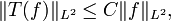Muckenhoupt weights
In mathematics, the class of Muckenhoupt weights 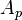 consists of those weights
consists of those weights 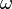 for which the Hardy–Littlewood maximal operator is bounded on
for which the Hardy–Littlewood maximal operator is bounded on 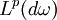 . Specifically, we consider functions
. Specifically, we consider functions  on
on  and their associated maximal functions
and their associated maximal functions  defined as
defined as
where 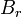 is a ball in
is a ball in  with radius
with radius  and centre
and centre  . We wish to characterise the functions
. We wish to characterise the functions 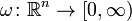 for which we have a bound
for which we have a bound
where  depends only on
depends only on 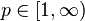 and
and 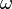 . This was first done by Benjamin Muckenhoupt.[1]
. This was first done by Benjamin Muckenhoupt.[1]
Definition
For a fixed 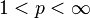 , we say that a weight
, we say that a weight 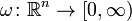 belongs to
belongs to 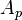 if
if  is locally integrable and there is a constant
is locally integrable and there is a constant  such that, for all balls
such that, for all balls  in
in  , we have
, we have
where  and
and 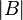 is the Lebesgue measure of
is the Lebesgue measure of  . We say
. We say 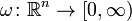 belongs to
belongs to  if there exists some
if there exists some  such that
such that
for all 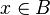 and all balls
and all balls  .[2]
.[2]
Equivalent characterizations
This following result is a fundamental result in the study of Muckenhoupt weights. A weight 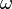 is in
is in 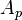 if and only if any one of the following hold.[2]
if and only if any one of the following hold.[2]
(a) The Hardy–Littlewood maximal function is bounded on 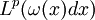 , that is
, that is
for some  which only depends on
which only depends on  and the constant
and the constant  in the above definition.
in the above definition.
(b) There is a constant  such that for any locally integrable function
such that for any locally integrable function  on
on 
for all balls  . Here
. Here
is the average of  over
over  and
and
Equivalently, 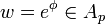 , where
, where 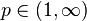 , if and only if
, if and only if
and
This equivalence can be verified by using Jensen's Inequality.
Reverse Hölder inequalities and 
The main tool in the proof of the above equivalence is the following result.[2] The following statements are equivalent
(a) 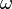 belongs to
belongs to 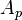 for some
for some 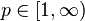
(b) There exists an  and a
and a  (both depending on
(both depending on 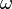 ) such that
) such that
for all balls 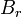
(c) There exists 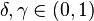 so that for all balls
so that for all balls  and subsets
and subsets 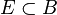
We call the inequality in (b) a reverse Hölder inequality as the reverse inequality follows for any non-negative function directly from Hölder's inequality. If any of the three equivalent conditions above hold we say  belongs to
belongs to  .
.
Weights and BMO
The definition of an 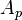 weight and the reverse Hölder inequality indicate that such a weight cannot degenerate or grow too quickly. This property can be phrased equivalently in terms of how much the logarithm of the weight oscillates:
weight and the reverse Hölder inequality indicate that such a weight cannot degenerate or grow too quickly. This property can be phrased equivalently in terms of how much the logarithm of the weight oscillates:
(a) If 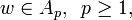 , then
, then 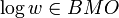 (i.e.
(i.e.  has bounded mean oscillation).
has bounded mean oscillation).
(b) If  , then for sufficiently small
, then for sufficiently small  , we have
, we have 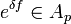 for some
for some  .
.
This equivalence can be established by using the exponential characterization of weights above, Jensen's inequality, and the John–Nirenberg inequality. Note that the smallness assumption on  in part (b) is necessary for the result to be true, as
in part (b) is necessary for the result to be true, as 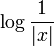 is a BMO function, but
is a BMO function, but 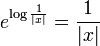 is not in any
is not in any 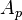 .
.
Further properties
Here we list a few miscellaneous properties about weights, some of which can be verified from using the definitions, others are nontrivial results:
(i) 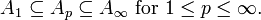
(ii) 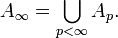
(iii) If 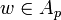 , then
, then 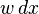 defines a doubling measure: for any ball B, if 2B is the ball of twice the radius, then
defines a doubling measure: for any ball B, if 2B is the ball of twice the radius, then 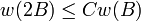 where C > 1 is a constant depending on
where C > 1 is a constant depending on  .
.
(iv) If 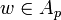 , then there is
, then there is  such that
such that 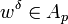 .
.
(v) If  then there is
then there is  and weights
and weights  such that
such that 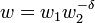 .[3]
.[3]
Boundedness of singular integrals
It is not only the Hardy–Littlewood maximal operator that is bounded on these weighted  spaces. In fact, any Calderón-Zygmund singular integral operator is also bounded on these spaces.[4] Let us describe a simpler version of this here.[2] Suppose we have an operator
spaces. In fact, any Calderón-Zygmund singular integral operator is also bounded on these spaces.[4] Let us describe a simpler version of this here.[2] Suppose we have an operator  which is bounded on
which is bounded on  , so we have
, so we have
for all smooth and compactly supported  . Suppose also that we can realise
. Suppose also that we can realise  as convolution against a kernel
as convolution against a kernel  in the sense that, whenever
in the sense that, whenever  and
and 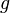 are smooth and have disjoint support
are smooth and have disjoint support
Finally we assume a size and smoothness condition on the kernel  :
:
for all 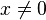 and multi-indices
and multi-indices  . Then, for each
. Then, for each 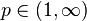 and
and  , we have that
, we have that  is a bounded operator on
is a bounded operator on  . That is, we have the estimate
. That is, we have the estimate
for all  for which the right-hand side is finite.
for which the right-hand side is finite.
A converse result
If, in addition to the three conditions above, we assume the non-degeneracy condition on the kernel  : For a fixed unit vector
: For a fixed unit vector 
whenever 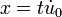 with
with 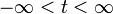 , then we have a converse. If we know
, then we have a converse. If we know
for some fixed 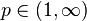 and some
and some 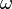 , then
, then  .[2]
.[2]
Weights and quasiconformal mappings
For  , a K-quasiconformal mapping is a homeomorphism
, a K-quasiconformal mapping is a homeomorphism 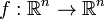 with
with 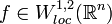 and
and
where 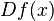 is the derivative of
is the derivative of  at
at  and
and  is the Jacobian.
is the Jacobian.
A theorem of Gehring[5] states that for all K-quasiconformal functions 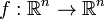 , we have
, we have 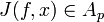 where
where  depends on
depends on  .
.
Harmonic measure
If you have a simply connected domain  , we say its boundary curve
, we say its boundary curve  is K-chord-arc if for any two points
is K-chord-arc if for any two points 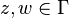 there is a curve
there is a curve  connecting
connecting  and
and  whose length is no more than
whose length is no more than 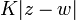 . For a domain with such a boundary and for any
. For a domain with such a boundary and for any 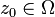 , the harmonic measure
, the harmonic measure 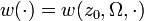 is absolutely continuous with respect to one-dimensional Hausdorff measure and its Radon–Nikodym derivative is in
is absolutely continuous with respect to one-dimensional Hausdorff measure and its Radon–Nikodym derivative is in  .[6] (Note that in this case, one needs to adapt the definition of weights to the case where the underlying measure is one-dimensional Hausdorff measure).
.[6] (Note that in this case, one needs to adapt the definition of weights to the case where the underlying measure is one-dimensional Hausdorff measure).
References
- Garnett, John (2007). Bounded Analytic Functions. Springer.
- ↑ Muckenhoupt, Benjamin (1972). "Weighted norm inequalities for the Hardy maximal function". Transactions of the American Mathematical Society, vol. 165: 207–226.
- ↑ 2.0 2.1 2.2 2.3 2.4 Stein, Elias (1993). "5". Harmonic Analysis. Princeton University Press.
- ↑ Jones, Peter W. (1980). "Factorization of Ap weights". Ann. Of Math. (2) 111 (3): 511–530. doi:10.2307/1971107.
- ↑ Grakakos, Loukas (2004). "9". Classical and Modern Fourier Analysis. New Jersey: Pearson Education, Inc.
- ↑ Gehring, F. W. (1973). "The Lp-integrability of the partial derivatives of a quasiconformal mapping". Acta Math. 130: 265–277. doi:10.1007/BF02392268.
- ↑ Garnett, John; Marshall, Donald (2008). Harmonic Measure. Cambridge University Measure.