Motion (geometry)

From Wikipedia, the free encyclopedia

In geometry, a motion is an isometry of a metric space. For instance, a plane with Euclidean distance as metric is a metric space in which a mapping associating congruent figures is a motion.[1] More generally, the term motion is a synonym for surjective isometry in metric geometry,[2] including elliptic geometry and hyperbolic geometry. In the latter case, hyperbolic motions provide an approach to the subject for beginners.

In differential geometry, a diffeomorphism is called a motion if it induces an isometry between the tangent space at a manifold point and the tangent space at the image of that point.[3][4]

Given a geometry, the set of motions forms a group under composition of mappings. This group of motions is noted for its properties. When the underlying space is a Riemannian manifold, the group of motions is a Lie group. Furthermore, the manifold has constant curvature if and only if, for every pair of points and every isometry, there is a motion taking one point to the other for which the motion induces the isometry.[5]

The idea of a group of motions for special relativity has been advanced as Lorentzian motions. For example, fundamental ideas have been laid out for a plane characterized by the quadratic form 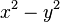x^{2}-y^{2}\ in American Mathematical Monthly.[6]

History

An early appreciation of the role of motion in geometry was given by Alhazen (965 to 1039). His work "Space and its Nature"[7] uses comparisons of the dimensions of a mobile body to quantify the vacuum of imaginary space.

In the 19th century Felix Klein became a proponent of group theory as a means to classify geometries according to their "groups of motions". He proposed using symmetry groups in his Erlangen program, a suggestion that was widely adopted. He noted that every Euclidean congruence is an affine mapping, and each of these is a projective transformation; therefore the group of projectivities contains the group of affine maps, which in turn contains the group of Euclidean congruencies. The term motion, shorter than transformation, puts more emphasis on the adjectives: projective, affine, Euclidean. The context was thus expanded, so much that "In topology, the allowed movements are continuous invertible deformations that might be called elastic motions."[8]

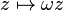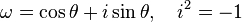The science of kinematics is dedicated to rendering physical motion into expression as mathematical transformation. Frequently the transformation can be written using vector algebra and linear mapping. A simple example is a turn written as a complex number multiplication: z\mapsto \omega z\ where \ \omega =\cos \theta +i\sin \theta ,\quad i^{2}=-1. Rotation in space is achieved by use of quaternions, and Lorentz transformations of spacetime by use of biquaternions. Early in the 20th century, hypercomplex number systems were examined. Later their automorphism groups led to exceptional groups such as G2.

In the 1890s logicians were reducing the primitive notions of synthetic geometry to an absolute minimum. Giuseppe Peano and Mario Pieri used the expression motion for the congruence of point pairs. Alessandro Padoa celebrated the reduction of primitive notions to merely point and motion in his report to the 1900 International Congress of Philosophy. It was at this congress that Bertrand Russell was exposed to continental logic through Peano. In his book Principles of Mathematics (1903), Russell considered a motion to be a Euclidean isometry that preserves orientation.[9]

Notes and references

  1. ↑ Gunter Ewald (1971) Geometry: An Introduction, p. 179, Belmont: Wadsworth ISBN0-534-0034-7
  2. ↑ M.A. Khamsi & W.A. Kirk (2001) An Introduction to Metric Spaces and Fixed Point Theorems, p. 15, John Wiley & Sons ISBN 0-471-41825-0
  3. ↑ A.Z. Petrov (1969) Einstein Spaces, p. 60, Pergamon Press
  4. ↑ B.A. Dubrovin, A.T. Fomenko, S.P Novikov (1992) Modern Geometry – Methods and Applications, second edition, p 24, Springer, ISBN 0-387-97993-9
  5. ↑ D.V. Alekseevskij, E.B. Vinberg, A.S. Solodonikov (1993) Geometry II, p. 9, Springer, ISBN 0-387-52000-7
  6. ↑ Graciela S. Birman & Katsumi Nomizu (1984) "Trigonometry in Lorentzian geometry", American Mathematical Monthly 91(9):543–9, group of motions: p 545
  7. ↑ Ibn Al_Haitham: Proceedings of the Celebrations of the 1000th Anniversary, Hakim Mohammed Said editor, pages 224-7, Hamdard National Foundation, Karachi: The Times Press
  8. ↑ Ari Ben-Menahem (2009) Historical Encyclopedia of the Natural and Mathematical Sciences, v. I, p. 1789
  9. ↑ B. Russell (1903) Principles of Mathematics p 418. See also pp 406, 436

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.