Mosco convergence
In mathematical analysis, Mosco convergence, is a notion of convergence for functionals that is used in nonlinear analysis and set-valued analysis. It is a particular case of Γ-convergence. Mosco convergence is sometimes phrased as “weak Γ-liminf and strong Γ-limsup” convergence since it uses both the weak and strong topologies on a topological vector space X.
Mosco convergence is named after Italian mathematician Umberto Mosco, a current Harold J. Gay[1] professor of mathematics at Worcester Polytechnic Institute.
Definition
Let X be a topological vector space and let X∗ denote the dual space of continuous linear functionals on X. Let Fn : X → [0, +∞] be functionals on X for each n = 1, 2, ... The sequence (or, more generally, net) (Fn) is said to Mosco converge to another functional F : X → [0, +∞] if the following two conditions hold:
- lower bound inequality: for each sequence of elements xn ∈ X converging weakly to x ∈ X,
- upper bound inequality: for every x ∈ X there exists an approximating sequence of elements xn ∈ X, converging strongly to x, such that
Since lower and upper bound inequalities of this type are used in the definition of Γ-convergence, Mosco convergence is sometimes phrased as “weak Γ-liminf and strong Γ-limsup” convergence. Mosco convergence is sometimes abbreviated to M-convergence and denoted by
References
- Mosco, Umberto (1967). "Approximation of the solutions of some variational inequalities". Ann. Scuola Normale Sup. (Pisa) 21: 373–394.
- Mosco, Umberto (1969). "Convergence of convex sets and of solutions of variational inequalities". Advances in Mathematics 3 (4): 510–585. doi:10.1016/0001-8708(69)90009-7.
- Borwein, Jonathan M.; Fitzpatrick, Simon (1989). "Mosco convergence and the Kadec property". Proc. Amer. Math. Soc. (American Mathematical Society) 106 (3): 843–851. doi:10.2307/2047444. JSTOR 2047444.
- Mosco, Umberto. "Worcester Polytechnic Institute Faculty Directory".
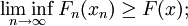
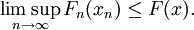
![{\mathop {{\text{M-lim}}}}_{{n\to \infty }}F_{{n}}=F{\text{ or }}F{\xrightarrow[ {n\to \infty }]{{\mathrm {M}}}}F.](/2014-wikipedia_en_all_02_2014/I/media/d/0/0/6/d0066f1a7111c39e6a79c83241aaa6d8.png)