Monge array

From Wikipedia, the free encyclopedia

In computer science, Monge arrays, or Monge matrices, are mathematical objects named for their discoverer, the French mathematician Gaspard Monge.

An m-by-n matrix is said to be a Monge array if, for all 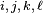$\scriptstyle i,\,j,\,k,\,\ell$ such that

$1\leq i<k\leq m{\text{ and }}1\leq j<\ell \leq n$

one obtains

$A[i,j]+A[k,\ell ]\leq A[i,\ell ]+A[k,j].\,$

So whenever we pick two rows and two columns of a Monge array (a 2 × 2 sub-matrix) and consider the four elements at the intersection points, the sum of the upper-left and lower right elements (across the main diagonal) is less than or equal to the sum of the lower-left and upper-right elements (across the antidiagonal).

This matrix is a Monge array:

${\begin{bmatrix}10&17&13&28&23\\17&22&16&29&23\\24&28&22&34&24\\11&13&6&17&7\\45&44&32&37&23\\36&33&19&21&6\\75&66&51&53&34\end{bmatrix}}$

For example, take the intersection of rows 2 and 4 with columns 1 and 5. The four elements are:

${\begin{bmatrix}17&23\\11&7\end{bmatrix}}$

17 + 7 = 24

23 + 11 = 34

The sum of the upper-left and lower right elements is less than or equal to the sum of the lower-left and upper-right elements.

Properties

The above definition is equivalent to the statement

A matrix is a Monge array if and only if $A[i,j]+A[i+1,j+1]\leq A[i,j+1]+A[i+1,j]$ for all $1\leq i<m$ and $1\leq j<n$ .

Any subarray produced by selecting certain rows and columns from an original Monge array will itself be a Monge array.

Any linear combination with non-negative coefficients of Monge arrays is itself a Monge array.

One interesting property of Monge arrays is that if you mark with a circle the leftmost minimum of each row, you will discover that your circles march downward to the right; that is to say, if $f(x)=\arg \min _{{i\in 1\ldots m}}A[x,i]$ , then $f(j)\leq f(j+1)$ for all $1\leq j<n$ . Symmetrically, if you mark the uppermost minimum of each column, your circles will march rightwards and downwards. The row and column maxima march in the opposite direction: upwards to the right and downwards to the left.

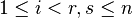The notion of weak Monge arrays has been proposed; a weak Monge array is a square n-by-n matrix which satisfies the Monge property $A[i,i]+A[r,s]\leq A[i,s]+A[r,i]$ only for all $1\leq i<r,s\leq n$ .
Every Monge array is totally monotone, meaning that its row minima occur in a nondecreasing sequence of columns, and that the same property is true for every subarray. This property allows the row minima to be found quickly by using the SMAWK algorithm.

Applications

A square Monge matrix which is also symmetric about its main diagonal is called a Supnick matrix (after Fred Supnick); this kind of matrix has applications to the traveling salesman problem (namely, that the problem admits of easy solutions when the distance matrix can be written as a Supnick matrix). Note that any linear combination of Supnick matrices is itself a Supnick matrix.

References

Deineko, Vladimir G.; Woeginger, Gerhard J. (October 2006). "Some problems around travelling salesmen, dart boards, and euro-coins" (PDF). Bulletin of the European Association for Theoretical Computer Science (EATCS) 90: 43–52. ISSN 0252-9742.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.