MoEDAL experiment

From Wikipedia, the free encyclopedia

Large Hadron Collider
(LHC)
LHC experiments

ATLAS	A Toroidal LHC Apparatus
CMS	Compact Muon Solenoid
LHCb	LHC-beauty
ALICE	A Large Ion Collider Experiment
TOTEM	Total Cross Section, Elastic Scattering and Diffraction Dissociation
LHCf	LHC-forward
MoEDAL	Monopole and Exotics Detector At the LHC
LHC preaccelerators
p and Pb	Linear accelerators for protons (Linac 2) and Lead (Linac 3)
(not marked)	Proton Synchrotron Booster
PS	Proton Synchrotron
SPS	Super Proton Synchrotron

The MoEDAL experiment is a physics experiment employing the Monopole and Exotics Detector at the Large Hadron Collider (LHC). It will share the cavern at Point 8 with LHCb, and its prime goal is to directly search for the magnetic monopole (MM)^[1]^[2] or dyon^[3] and other highly ionizing stable massive particles (SMPs) and pseudo-stable massive particles. To detect these particles, the project will use nuclear track detectors (NTDs), which suffer characteristic damage due to highly ionizing particles. As MMs and SMPs are highly ionizing, NTDs are perfectly suited for the purpose of detection.

It is an international research collaboration whose spokesperson is the University of Alberta’s James Pinfold. It is the seventh experiment at the LHC, was approved and sanctioned by the CERN research board on May 2010, and started its first test deployment in January 2011.^[4]

Background

The search for highly ionizing SMPs at the LHC can be divided into three main categories. The first category is that of massive magnetically charged particles such as the magnetic monopole or the dyon. Another open question in modern physics is the existence of SMPs with single electrical charge providing a second category of particle that is heavily ionizing by virtue of its small $\beta$ , where $\beta ={\tfrac {v}{c}}$ .

The most obvious possibility for an SMP is that one or more new states exist which carry a new conserved, or almost conserved, global quantum number. SUSY with R-parity, extra dimensions with KK-parity, and several other models fall into this category. The lightest of the new states will be stable, due to the conservation of this new parity, and depending on quantum numbers, mass spectra, and interaction strengths, one or more higher-lying states may also be stable or meta-stable. The third class of hypothetical particle has multiple electric charge such as the black hole remnant, or long-lived doubly charged Higgs boson.

SMPs with magnetic charge, single or multiple electric charge and with 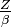${\tfrac {Z}{\beta }}$ (Z is electric charge number) as low as five can in principle be detected by the CR39 NTDs, putting them within the physics reach of the MoEDAL experiment.

The search for the magnetic monopole

In 1931 Dirac introduced the magnetic monopole in order to explain the quantization of the electric charge, which follows from the existence of at least one free magnetic charge. He established the basic relationship between the elementary electric charge e and the basic magnetic charge:

$g={\frac {n\hbar c}{2e}}=ng_{D}$

where n is an integer, n = 1, 2, ... The magnetic charge 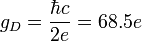$g=ng_{D}$ ; $g_{D}={\frac {\hbar c}{2e}}=68.5e$ is called the unit Dirac charge. The existence of magnetic charges and of magnetic currents would symmetrize in form Maxwell’s equations, but the symmetry would not be perfect since $e\neq g$ . But, if the couplings are energy dependent they could converge to a single common value at very high energies.

There is no real prediction of the mass of classical Dirac magnetic monopole. One may obtain a rough estimate assuming that the classical monopole radius is equal to the classical electron radius: from which 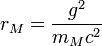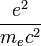$r_{M}={\frac {g^{{2}}}{m_{M}c^{{2}}}}$ = $r_{e}$ = ${\frac {e^{{2}}}{m_{e}c^{{2}}}}$ from which 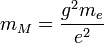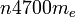$m_{M}={\frac {g^{{2}}m_{e}}{e^{{2}}}}$ ~ $n4700m_{e}$ = ${\frac {n2.4GeV}{c^{{2}}}}$ . 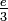Thus the mass should be relatively large and even larger if the basic charge is ${\tfrac {e}{3}}$ (the quark charge) and if n > 1.

Grand unification magnetic monopoles, with masses of the order of 10¹⁵ GeV are well beyond the reach of any presently conceivable man-made accelerator. Nevertheless, there are models where monopoles could appear in a mass range accessible to the LHC. Examples include:

The electroweak Cho-Maison monopole; The Troost-Vinciarelli monopole with mass that depends on the matter field (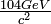 ${\tfrac {104GeV}{c^{{2}}}}$ with IVB matter fields, 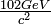${\tfrac {102GeV}{c^{{2}}}}$ with matter fields and 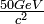${\tfrac {50GeV}{c^{{2}}}}$ with spin-1/2 matter fields); Some superstring models where, monopoles/dyons with a mass low enough (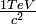 ${\tfrac {1TeV}{c^{{2}}}}$ ) to be detected at the LHC are hypothesized.

Since 1931 searches for magnetic monopoles have been carried out at each new accelerator at the high energy frontier. Relatively simple search experiments were employed and recently also large collider detectors were used. In fact, monopole searches have been carried out in e+-e-, e-p, p-p, and p-pbar interactions at various high energy colliders. For example, searches at the Fermilab collider seem to exclude magnetic monopoles with masses up to 850 GeV. Experiments at the LEP2 collider excluded masses below 102 GeV. The limits produced on magnetic monopole production depend on the physical process by which the monopole is presumed to be produced.

The search for SMPs

Generic SMPs which possess electric charge and penetrate through the ATLAS or CMS detector will leave a clear signature of a high-pT, slow, muon-like track. The background is expected to be highly suppressed by use of the time of flight technique. Thus, penetrating SMPs with appropriate production cross sections would, in principle, be observed. However, as mentioned above, for an SMP at the LHC to be detected or triggered in a certain detector system and be associated to the correct bunch crossing, it should arrive at most 25 ns after the default arrival time of a particle traveling at the speed of light. Later arrival would imply triggering or detection within a subsequent crossing time window. This would complicate detection.

For SMPs which stop in the calorimeter and do not traverse the muon system, searches could rely on observing an excess of high-pT tracks in the inner detectors. In conjunction with this, observable such as a charged particle leaving a signature of anomalous ionization in the tracking chambers together with a characteristic energy deposition profile in the calorimeters could also be used. However, highly ionizing SMPs can be absorbed before they penetrate ATLAS or CMS. Also, as described earlier the precision with which ionization energy loss can be measured in the general purpose LHC detectors is not clear.

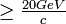An example of a study of the possible detection of SMPs at the LHC assumes a proposed ATLAS high luminosity trigger ( $1034cm^{{-2}}s^{{-1}}$ ) and high pT ( $\geq {\tfrac {20GeV}{c}}$ ) muons in which all the three stations of the ATLAS RPC are in coincidence. Figure 5 shows the trigger efficiency they obtained. The efficiency drops rapidly from 50% at a 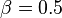$\beta =0.5$ to zero at $\beta =0.35$ . 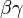In the Figure above the delay (ns/m) of the SMP particle with respect to an ultra-relativistic particle as a function of $\beta$ and $\beta \gamma$ is reported. As the outermost muon chambers extend to radius of 10m in ATLAS, we can see that the SMP does not reach them during a single beam crossing period of 25ns. In the lower Figure the corresponding energy loss rate normalized to its minimum value is shown. As can be seen an SMP would be detectable with NTDs with a 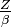${\tfrac {Z}{\beta }}$ threshold of 5 at a 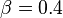$\beta =0.4$ . The rapid increase of the energy loss with decreasing values means that the SMP particle may stop inside the hadronic calorimeter.

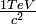In the figure below we can see the range of an SMP particle in iron is given as a function of $\beta$ , for a mass of 0.2, 0.6 and ${\tfrac {1TeV}{c^{{2}}}}$ . Considering that the inner ATLAS calorimeter system corresponds to about 2 m of iron, we see that only SMP particles with masses M $\geq {\tfrac {1TeV}{c^{{2}}}}$ could escape the calorimeter when $\leq$ 0.25. An SMP particle stopped inside the calorimeter is typically lost because the kinetic energy deposited into the calorimeter is, in almost every case, below the threshold of the hadron calorimeter trigger.

The MoEDAL experiment would be able to complement the above search strategies by allowing searches for electrically charged SMPs with 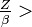${\tfrac {Z}{\beta }}>$ 5, with a maximum around 200e $\rightarrow$ 300e. The upper limit on the SMP 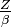${\tfrac {Z}{\beta }}$ to which ATLAS and CMS will be sensitive is still unclear. However, it is likely to be substantially below the reach of MoEDAL.

Detecting magnetic monopoles and stable massive particles

The MoEDAL detector is an array of plastic NTDs deployed around the Point-8 intersection region of the LHCb detector, in the VELO (vertex locator) cavern. The array consists of NTD stacks, ten layers deep, in aluminium housings attached to the walls and ceiling of the VELO cavern. The maximum possible surface area available for detectors is around 25 m², although the final deployed area could be somewhat less due to the developing requirements of the infrastructure of the LHCb detector. A more detailed description of the MoEDAL detectors and the track-etch detector technology, can be found in the MoEDAL technical design document.

When a charged particle crosses a plastic nuclear track detector it produces damages at the level of polymeric bonds in a small cylindrical region around its trajectory forming the so-called latent track. The damage produced is dependent on the energy released inside the cylindrical region, i.e. the restricted energy loss (REL), which is a function of the charge Z and $\beta ={\tfrac {v}{c}}$ (c the velocity of light in vacuum) of the incident highly ionizing particle (ion). 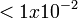When the velocity of the incident ion is $<1x10^{{-2}}$ c the REL is equal to the total energy loss of the particle in the medium; otherwise, only a fraction of the electronic energy loss leading to the formation of d-rays with energies lower than a cut-off energy $T_{{cut}}$ cut is efficient for the track formation. The REL can be computed from the Bethe-Bloch formula restricted to energy transfers T 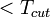$<T_{{cut}}$ .... The subsequent etching of the solid nuclear detectors leads to the formation of etch-pit cones. These conical pits are usually of micrometer dimensions and can be observed with an optical microscope. Their size and shape yield information about charge, energy and direction of motion of the incident ion. The NTDs will be detecting the SMPs and magnetic monopoles, but in order to detect anything, noise and background must be removed. To do this, alternating layers of NTDs (CR39 films and MAROFOLs) and Lexan brand plastic are placed in the detection zone.^[5] The NTDs are radiation hard, which means they are resistant to ionizing radiation. Needless to say, this quality will be priceless in an environment where energies are on the scale of tera-electron volts, which will produce cascading particle creations and annihilations which in turn will release tremendous energies. 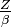They are also calibrated to very high values of ${\tfrac {Z}{\beta }}$ , which means they are sensitive to particles that are highly ionizing either by being multiplely charged or slow moving (or both). The Lexan sheets are for impact protection. Lexan is commonly used in bullet-proof windows. To put the strengths of the electromagnetic fields into perspective, we can compare the ionization caused by a Dirac charge to that of a unit electric charge (electron’s charge). The force of the magnetic field is about 4700 times stronger than the electric field. This will make a characteristic mark on the NTDs. If the NTDs are soaked in a caustic solution, the tracks made by the magnetic monopoles or SMPs will be amplified into readily visible “holes”. When the NTDs are set back into their original configuration, a pathway and ionization effect can be calculated for the “holes” made by the magnetic monopoles or SMPs. This will be enough information to determine a monopole event or SMP event. Just one event will be enough to determine the existence of magnetic monopoles, or a possibly new SMP.

Detector Summary

The basic detector unit of the MoEDAL experiment is a stack of ten sheets of plastic NTDs, consisting of 4 sheets of CR39 (polyallyl diglycol carbonate - PADC), each ~ 0.5 mm thick, 3 sheets of MAKROFOL (lexan (each ~0.5mm thick) with Lexan (each ~0.2mm thick) forming the first, middle and end sheets of the stack.

The basic MoEDAL detector units are deployed in aluminium housings that hold 6 basic MoEDAL NTD stacks. The aluminium housing is 1.00 mm thick aluminium. The size of the housing is approximately 50 cm x 75 cm with a depth of approximately 2 cm. The weight of the housing when full of detectors is around 8 kg. Commercially pure aluminium alloy (1100) is utilized throughout the MoEDAL detector in order to reduce activation.

For highly ionizing particles such as fast magnetic monopoles the REL of the incident particle will be constant along the trajectory of the monopole through the detector sheets. Thus, etch pit cones will be collinear and equally sized, throughout the NTD stack. This energy loss signature is easily distinguished from background of low energy particles which are slowed down and even absorbed inside the detector. In this case the etch-pit size changes (increases) along the trajectory as it loses energy.

Detector Mounting Scheme

The detector mounting system is a set of aluminium rails onto which the aluminium detector housings can be screwed. The mounting rails are cut to length and have cross-section 2.5 cm x 1.9 cm (deep). They are pre-drilled with two sets of holes: attachment holes that enable the rail to be attached to the concrete, in this case we have a hole for every metre of rail; and, a second set of holes, drilled every 10 cm that are used for attaching the detector housing to the frame, using M4 screws through each corner of the housing. The rails are mounted using “ Hilti” 3/8” inserts with 1/4” (diam.) screws. Each mounting point is rated to take a load of 200 kg.

After the detectors have been mounted in their various housings their position is fixed with respect to the rigid wall mounted MoEDAL framework. The position of the framework on each surface of the VELO cavern is recorded by survey marks attached to at least two detector housing attached to that framework. The accuracy of the registration of a highly ionizing track in a stack combined with the accuracy with which we can place the track in the space, allows us point this track from its position near to the VELO wall, or ceiling, back to the LHCb IP with an accuracy of ~ 1 cm.

It is envisaged that the Phase1 the installation of the full detector will take around 4 working days. First, the rail mounting described directly above, will be attached to the wall. The detector assemblies that are 2.5 cm deep, measure 50 x 75 cm and weigh about 8 kg when full of detectors, will be attached to the rails by M4 screws. These assemblies look like flat shallow aluminium boxes.

Calibration

By exposing the detector to relativistic heavy ions of known energy and electric charge. it is possible to obtain the calibration data expressed as the reduced etching rate (p - 1) versus REL. So, the charge of an incoming particle can be determined by the measured p of the corresponding tracks. Only particles releasing a REL above a threshold and incident within a definite angle (which depends on the particle energy loss) will be detected. Specific processing and etching conditions affect the detector threshold 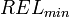$REL_{{min}}$ , or $\left({\tfrac {Z}{\beta }}\right)_{{min}}$ that is the minimum charge and speed a particle must have to produce an etchable latent track.

A typical calibration set-up at an ion beam accelerator includes a fragmentation target and nuclear track detector foils in front of and behind a target. The ion beam passes through some detector foils, interacts in the target (typically 10 mm thick Cu or Al plates) and then traverses downstream detector foils which record the survived fraction of original projectiles, as well as their fragments. The projectile fragments carry the same and approximately the same direction of the incident ion; the Z of each resolved peak is identified via the base area spectrum. After exposure the detector sheets are etched in standard conditions.

The calibration of the plastic will take place at the CERN North Area, or at the Brookhaven National Laboratory (BNL), using a heavy ion test beam. If this option is not available another heavy ion test beam facility [89] will be utilized. The aim is to calibrate each batch of plastic supplied to MoEDAL. If possible a number of individual sheets will be ”tagged” by exposing a corner of the detector sheets at a heavy-ion beam facility prior to exposure at Point 8. The analysis of the exposed plastic requires that a number of sheets of plastic will need to be etched under differing etching conditions. Also, the positions of individual plastic sheets within a stack will need to be tracked, as well as the position of the stack within the MoEDAL detector array.

The Etching Process

Two procedures, based on experience with the SLIM experiment [88], have been defined for the chemical etching of CR 39 detectors: the strong and soft etching conditions:

1. The strong etching conditions for CR 39 are 8N KOH+1.5% ethyl alcohol at 75C for 30 h. It is applied t quickly remove a large amount of material allowing a better surface quality and larger post-etched cones making them easier to detect during visual scanning; The soft etching conditions for CR 39 are 6N NaOH+1% ethyl alcohol at 70C for 40 h. It allows etching to proceed in several etching steps in order to study the formation of the post-etched cones giving reliable measurements of the deposited energy and the direction of the incident particle. The addition of ethyl alcohol in the etchant increases the detection threshold, but it improves the etched surface quality and reduces the number of surface defects and background tracks.

2. The threshold for CR39 is 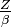${\tfrac {Z}{\beta }}$ ~ 14 in strong etching corresponding to a minimum 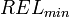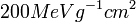$REL_{{min}}$ ~ $200MeVg^{{-1}}cm^{{2}}$ . In soft etching conditions the threshold is at 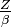${\tfrac {Z}{\beta }}$ ~ 7 which corresponds to 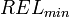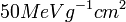$REL_{{min}}$ ~ $50MeVg^{{-1}}cm^{{2}}$ . 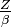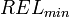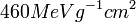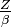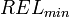In the case where CR 39 is polymerized with 0.1% DOP additive the thresholds are raised to ${\tfrac {Z}{\beta }}$ ~ 21 ( $REL_{{min}}$ ~ $460MeVg^{{-1}}cm^{{2}}$ ) for strong etching and to ${\tfrac {Z}{\beta }}$ ~ 13 ( $REL_{{min}}$ ~ $170MeVg^{{-1}}cm^{{2}}$ ) for soft etching. 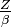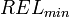The etching conditions for Makrofol are 6N KOH + 20% ethyl alcohol at 50C for 10 h, and the corresponding threshold is ${\tfrac {Z}{\beta }}$ ~50, $REL_{{min}}$ ~ $2.5GeVg^{{-1}}cm^{{2}}$ . The chemical etching is performed in the Nuclear Track Etch Detector Laboratory of INFN, in Bologna. 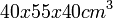Stainless steel tanks are used: two large tanks of $40x55x40cm^{{3}}$ dimensions, a medium tank 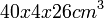$40x4x26cm^{{3}}$ and two small tanks 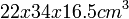$22x34x16.5cm^{{3}}$ having different types of stirring and heating systems and of temperature control. The stability of the etching temperature throughout the solution is maintained to within 0.01%. The detector foils are placed in the stainless steel detector holders in the etching solution inside the tanks. There are three other tanks which are used for the presoaking and washing of the detectors.

References

↑ P.A.M. Dirac, Proc. R. Soc. London, Set. A, 133, 60 (1931); P.A.M. Dirac, Phys. Tev., 24, 817 (1948)
↑ G. Giacomelli and M. Sioli (Astroparticle Physics), Lectures at the 2002 Int. School of Physics, Constantine, Algeria, hep-ex/0211035; G. Giacomelli and L. Patrizii, hepex/ 011209; G.R. Kalbfleisch, Phys. Rev. Lett. 85, 5292 (2000); hep-ex/0005005 ; K. A. Milton et al., hep-ex/0009003; B. Abbott et al., hep-ex/9803023, Phys. Rev. Lett. 81, 524 (1998); G. Giacomelli, Riv. Nuovo Cimento 7 N.12, 1 (1984); M. Acciarri et al., Phys. Lett. B345, 609 (1995); L. Gamberg et al., hep-ph/9906526
↑ J. Schwinger, Science, Volume 165, Issue 3895, 757 (1969)
↑ CERN Courier, "MoEDAL becomes the LHC's magnificent seventh", 5 May 2010
↑ Pinfold, J. L., “ The MoEDAL-LHC Experiment”, Lecture given to the Cavendish Society (2010). Obtained from James Pinfold via email. (Similar material under MoEDAL webpage)

External links

http://moedal.web.cern.ch/

European Organization for Nuclear Research (CERN)

Large Hadron Collider

LHC	List of LHC experiments ALICE ATLAS CASTOR CMS FP420 HV-QF LHCb LHCf MoEDAL TOTEM

Large Electron–Positron Collider

LEP	List of LEP experiments ALEPH DELPHI OPAL L3 LEP5 LEP6

Super Proton Synchrotron

SPS	List of SPS experiments CNGS NA48 NA49 NA58/COMPASS NA60 NA61/SHINE NA62 UA1 UA2

Proton Synchrotron

PS	AD Proton Synchrotron Booster AIDA DIRAC ELENA ISOLDE ISOLTRAP MISTRAL WITCH

Linear Accelerators

CTF3
LINAC
LINAC 2
LINAC 3
LINAC 4

Others Accelerators & Experiments

Future projects

LHC@home
Safety of high energy particle collision experiments

Coordinates: 46°14′09″N 6°03′18″E / 46.235753°N 6.055092°E / 46.235753; 6.055092

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.