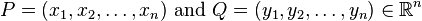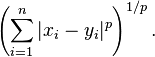Minkowski distance

From Wikipedia, the free encyclopedia

The Minkowski distance is a metric on Euclidean space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance.

Definition

The Minkowski distance of order p between two points

P=(x_{1},x_{2},\ldots ,x_{n}){\text{ and }}Q=(y_{1},y_{2},\ldots ,y_{n})\in {\mathbb {R}}^{n}

is defined as:

\left(\sum _{{i=1}}^{n}|x_{i}-y_{i}|^{p}\right)^{{1/p}}.

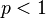For p\geq 1, the Minkowski distance is a metric as a result of the Minkowski inequality. For p<1, it is not - the distance between (0,0) and (1,1) is 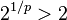2^{{1/p}}>2, but the point (0,1) is a distance 1 from both of these points. Hence, this violates the triangle inequality.

Minkowski distance is typically used with p being 1 or 2. The latter is the Euclidean distance, while the former is sometimes known as the Manhattan distance. In the limiting case of p reaching infinity, we obtain the Chebyshev distance:

\lim _{{p\to \infty }}{\left(\sum _{{i=1}}^{n}|x_{i}-y_{i}|^{p}\right)^{{\frac {1}{p}}}}=\max _{{i=1}}^{n}|x_{i}-y_{i}|.\,

Similarly, for p reaching negative infinity, we have:

\lim _{{p\to -\infty }}{\left(\sum _{{i=1}}^{n}|x_{i}-y_{i}|^{p}\right)^{{\frac {1}{p}}}}=\min _{{i=1}}^{n}|x_{i}-y_{i}|.\,

The Minkowski distance can also be viewed as a multiple of the power mean of the component-wise differences between P and Q.

The following figure shows unit circles with various values of p:

See also

External links

Simple IEEE 754 implementation in C++

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.