Midpoint-stretching polygon
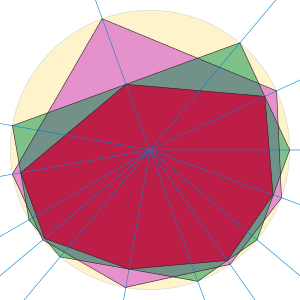
In geometry, the midpoint-stretching polygon of a cyclic polygon P is another cyclic polygon inscribed in the same circle, the polygon whose vertices are the midpoints of the circular arcs between the vertices of P.[1] It may be derived from the midpoint polygon of P (the polygon whose vertices are the edge midpoints) by placing the polygon in such a way that the circle's center coincides with the origin, and stretching or normalizing the vector representing each vertex of the midpoint polygon to make it have unit length.
The midpoint-stretching polygon is also called the shadow of P; when the circle is used to describe a repetitive time sequence and the polygon vertices on it represent the onsets of a drum beat, the shadow represents the set of times when the drummer's hands are highest, and has greater rhythmic evenness than the original rhythm.[2]
The midpoint-stretching polygon of a regular polygon is itself regular, and iterating the midpoint-stretching operation on an arbitrary initial polygon results in a sequence of polygons whose shape converges to that of a regular polygon.[1][3]
References
- ↑ 1.0 1.1 Ding, Jiu; Hitt, L. Richard; Zhang, Xin-Min (1 July 2003), "Markov chains and dynamic geometry of polygons", Linear Algebra and its Applications 367: 255–270, doi:10.1016/S0024-3795(02)00634-1, retrieved 19 October 2011.
- ↑ Gomez-Martin, Francisco; Taslakian, Perouz; Toussaint, Godfried T. (2008), "Evenness preserving operations on musical rhythms", Proceedings of the 2008 C3S2E conference, doi:10.1145/1370256.1370275.
- ↑ Gomez-Martin, Francisco; Taslakian, Perouz; Toussaint, Godfried T. (2008), "Convergence of the shadow sequence of inscribed polygons", 18th Fall Workshop on Computational Geometry