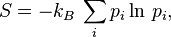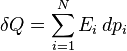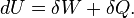Microstate (statistical mechanics)

From Wikipedia, the free encyclopedia

In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature and pressure.^[1] Treatments on statistical mechanics, ^[2] ^[3] often give an equivalent definition of a macrostate by specifying it for an isolated thermodynamic system. A particular set of values of energy, number of particles and volume of an isolated thermodynamic system is said to specify a particular macrostate of it. In this description, microstates appear as different possible ways the system can achieve a particular macrostate.

A macrostate is characterized by a probability distribution of possible states across a certain statistical ensemble of all microstates. This distribution describes the probability of finding the system in a certain microstate. In the thermodynamic limit, the microstates visited by a macroscopic system during its fluctuations all have the same macroscopic properties.

Microscopic definitions of thermodynamic concepts

Statistical mechanics links the empirical thermodynamic properties of a system to the statistical distribution of an ensemble of microstates. All macroscopic thermodynamic properties of a system may be calculated from the partition function that sums the energy of all its microstates.

At any moment a system is distributed across an ensemble of N microstates, each denoted by i, and having a probability of occupation p_i, and an energy $E_{i}$ . These microstates form a discrete set as defined by quantum statistical mechanics, and $E_{i}$ is an energy level of the system.

Internal energy

The internal energy of the macrostate is the mean over all microstates of the system's energy

$U=\langle E\rangle =\sum _{{i=1}}^{N}p_{i}\,E_{i}\ .$

This is a microscopic statement of the notion of energy associated with the first law of thermodynamics.

Entropy

The absolute entropy exclusively depends on the probabilities of the microstates and is defined as

$S=-k_{B}\,\sum _{i}p_{i}\ln \,p_{i},$

where $k_{B}$ is Boltzmann's constant, for the canonical ensemble. For the microcanonical ensemble, consisting of only those microstates with energy equal to the energy of the macrostate, this simplifies to

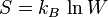$S=k_{B}\,\ln W$ ,

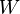where $W$ is the number of microstates. This form for entropy appears on Ludwig Boltzmann's gravestone in Vienna.

The second law of thermodynamics describes how the entropy of an isolated system changes in time. The third law of thermodynamics is consistent with this definition, since zero entropy means that the macrostate of the system reduces to a single microstate.

Heat and work

Heat is the energy transfer associated with a disordered, microscopic action on the system, associated with jumps in energy levels of the system.

Work is the energy transfer associated with an ordered, macroscopic action on the system. If this action acts very slowly then the Adiabatic theorem implies that this will not cause a jump in the energy level of the system. The internal energy of the system can only change due to a change of the energies of the system's energy levels.

The microscopic definitions of heat and work are the following:

$\delta W=\sum _{{i=1}}^{N}p_{i}\,dE_{i}$

$\delta Q=\sum _{{i=1}}^{N}E_{i}\,dp_{i}$

so that

$~dU=\delta W+\delta Q.$

The two above definitions of heat and work are among the few expressions of statistical mechanics where the sum corresponding to the quantum case cannot be converted into an integral in the classical limit of a microstate continuum. The reason is that classical microstates are usually not defined in relation to a precise associated quantum microstate, which means that when work changes the energy associated to the energy levels of the system, the energy of classical microstates doesn't follow this change.

References

↑ Macrostates and Microstates
↑ Reif, Frederick (1965). Fundamentals of Statistical and Thermal Physics. McGraw-Hill. p. 66. ISBN 07-051800-9 Check |isbn= value (help).
↑ Pathria, R K (1965). Statistical Mechanics. Butterworth-Heinemann. p. 10. ISBN 0-7506-2469-8.

External links

Some illustrations of microstates vs. macrostates

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.