Meta-analysis

From Wikipedia, the free encyclopedia

In statistics, a meta-analysis refers to methods that focus on contrasting and combining results from different studies, in the hope of identifying patterns among study results, sources of disagreement among those results, or other interesting relationships that may come to light in the context of multiple studies.[1] In its simplest form, meta-analysis is normally done by identification of a common measure of effect size. A weighted average of that common measure is the output of a meta-analysis. The weighting is related to sample sizes within the individual studies. More generally there are other differences between the studies that need to be allowed for, but the general aim of a meta-analysis is to more powerfully estimate the true effect size as opposed to a less precise effect size derived in a single study under a given single set of assumptions and conditions. A meta-analysis therefore gives a thorough summary of several studies that have been done on the same topic, and provides the reader with extensive information on whether an effect exists and what size that effect has.

Meta-analyses are often, but not always, important components of a systematic review procedure. For instance, a meta-analysis may be conducted on several clinical trials of a medical treatment, in an effort to obtain a better understanding of how well the treatment works. Here it is convenient to follow the terminology used by the Cochrane Collaboration,[2] and use "meta-analysis" to refer to statistical methods of combining evidence, leaving other aspects of 'research synthesis' or 'evidence synthesis', such as combining information from qualitative studies, for the more general context of systematic reviews.

Meta-analysis forms part of a framework called estimation statistics which relies on effect sizes, confidence intervals and precision planning to guide data analysis, and is an alternative to null hypothesis significance testing.

History

A historical instance of Meta-analysis dates back to the twelfth century in China, a famous philosopher, Chu Hsi (朱熹, 1130~1200), built up his philosophical theory by summarizing a series of related literatures. He called this research methodology 'Theory of Systematic Rule'(道統論) (See reference http://ir.lib.ntnu.edu.tw/retrieve/52215/). While in the Western World, the historical roots of meta-analysis may be traced back to 17th century studies of astronomy, a paper published in 1904 by the statistician Karl Pearson in the British Medical Journal which collated data from several studies of typhoid inoculation is seen as the first time a meta-analytic approach was used to aggregate the outcomes of multiple clinical studies.[3][4] The first meta-analysis of all conceptually identical experiments concerning a particular research issue, and conducted by independent researchers, has been identified as the 1940 book-length publication Extra-sensory perception after sixty years, authored by Duke University psychologists J. G. Pratt, J. B. Rhine, and associates.[5] This encompassed a review of 145 reports on ESP experiments published from 1882 to 1939, and included an estimate of the influence of unpublished papers on the overall effect (the file-drawer problem). Although meta-analysis is widely used in epidemiology and evidence-based medicine today, a meta-analysis of a medical treatment was not published until 1955. In the 1970s, more sophisticated analytical techniques were introduced in educational research, starting with the work of Gene V. Glass, Frank L. Schmidt and John E. Hunter.

The term "meta-analysis" was coined by Gene V. Glass,[6] who was the first modern statistician to formalize the use of the term meta-analysis. He states "my major interest currently is in what we have come to call ...the meta-analysis of research. The term is a bit grand, but it is precise and apt ... Meta-analysis refers to the analysis of analyses". Although this led to him being widely recognized as the modern founder of the method, the methodology behind what he termed "meta-analysis" predates his work by several decades.[7][8] The statistical theory surrounding meta-analysis was greatly advanced by the work of Nambury S. Raju, Larry V. Hedges, Harris Cooper, Ingram Olkin, John E. Hunter, Jacob Cohen, Thomas C. Chalmers, Robert Rosenthal and Frank L. Schmidt.

Advantages of meta-analysis

Conceptually, a meta-analysis uses a statistical approach to combine the results from multiple studies. Its advantages can therefore be interpreted as follows:

  • Results can be generalized to a larger population,
  • The precision and accuracy of estimates can be improved as more data is used. This, in turn, may increase the statistical power to detect an effect.
  • Inconsistency of results across studies can be quantified and analyzed. For instance, does inconsistency arise from sampling error, or are study results (partially) influenced by between-study heterogeneity.
  • Hypothesis testing can be applied on summary estimates,
  • Moderators can be included to explain variation between studies,
  • The presence of publication bias can be investigated,

Pitfalls

A meta-analysis of several small studies does not predict the results of a single large study.[9] Some have argued that a weakness of the method is that sources of bias are not controlled by the method: a good meta-analysis of badly designed studies will still result in bad statistics.[10] This would mean that only methodologically sound studies should be included in a meta-analysis, a practice called 'best evidence synthesis'.[10] Other meta-analysts would include weaker studies, and add a study-level predictor variable that reflects the methodological quality of the studies to examine the effect of study quality on the effect size.[11] However, others have argued that a better approach is to preserve information about the variance in the study sample, casting as wide a net as possible, and that methodological selection criteria introduce unwanted subjectivity, defeating the purpose of the approach.[12]

Publication bias: the file drawer problem

A funnelplot expected without the file drawer problem. The largest studies converge on a null result, while smaller studies show more random variability.
A funnelplot expected with the file drawer problem. The largest studies still cluster around the null result, but the bias against publishing negative studies has caused the literature as a whole to appear unjustifiably favourable to the hypothesis.

Another potential pitfall is the reliance on the available corpus of published studies, which may create exaggerated outcomes due to publication bias, as studies which show negative results or insignificant results are less likely to be published. For example, one may have overlooked dissertation studies or studies that have never been published. This is not easily solved, as one cannot know how many studies have gone unreported.[13]

This file drawer problem results in the distribution of effect sizes that are biased, skewed or completely cut off, creating a serious base rate fallacy, in which the significance of the published studies is overestimated, as other studies were either not submitted for publication or were rejected. This should be seriously considered when interpreting the outcomes of a meta-analysis.[13][14]

The distribution of effect sizes can be visualized with a funnel plot which is a scatter plot of sample size and effect sizes. In fact, for a certain effect level, the smaller the study, the higher is the probability to find it by chance. At the same time, the higher the effect level, the lower is the probability that a larger study can result in that positive result by chance. If many negative studies were not published, the remained positive studies give rise to a funnel plot in which effect size is inversely proportional to sample size, in other words: the higher the effect size, the smaller the sample size. An important part of the shown effect is then due to chance that is not balanced in the plot because of unpublished negative data absence. In contrast, when most studies were published, the effect shown has no reason to be biased by the study size, so a symmetric funnel plot results. So, if no publication bias is present, one would expect that there is no relation between sample size and effect size.[15] A negative relation between sample size and effect size would imply that studies that found significant effects were more likely to be published and/or to be submitted for publication. There are several procedures available that attempt to correct for the file drawer problem, once identified, such as guessing at the cut off part of the distribution of study effects.

Methods for detecting publication bias have been controversial as they typically have low power for detection of bias, but also may create false positives under some circumstances.[16] For instance small study effects, wherein methodological differences between smaller and larger studies exist, may cause differences in effect sizes between studies that resemble publication bias. However, small study effects may be just as problematic for the interpretation of meta-analyses, and the imperative is on meta-analytic authors to investigate potential sources of bias. A Tandem Method for analyzing publication bias has been suggested for cutting down false positive error problems.[17] This Tandem method consists of three stages. Firstly, one calculates Orwin's fail-safe N, to check how many studies should be added in order to reduce the test statistic to a trivial size. If this number of studies is larger than the number of studies used in the meta-analysis, it is a sign that there is no publication bias, as in that case, one needs a lot of studies to reduce the effect size. Secondly, one can do an Egger's regression test, which tests whether the funnel plot is symmetrical. As mentioned before: a symmetrical funnel plot is a sign that there is no publication bias, as the effect size and sample size are not dependent. Thirdly, one can do the trim-and-fill method, which imputes data if the funnel plot is asymmetrical. Important to note is that these are just a couple of methods that can be used, but several more exist.

Nevertheless, it is suggested that 25% of meta-analyses in the psychological sciences may have publication bias.[17] However, low power problems likely remain at issue, and estimations of publication bias may remain lower than the true amount.

Most discussions of publication bias focus on journal practices favoring publication of statistically significant finds. However, questionable researcher practices, such as reworking statistical models until significance is achieved, may also favor statistically significant findings in support of researchers' hypotheses[18][19] Questionable researcher practices aren't necessarily sample size dependent, and as such are unlikely to be evident on a funnel plot and may go undetected by most publication bias detection methods currently in use.

Other weaknesses are Simpson's paradox (two smaller studies may point in one direction, and the combination study in the opposite direction) and subjectivity in the coding of an effect or decisions about including or rejecting studies.[20] There are two different ways to measure effect: correlation or standardized mean difference. The interpretation of effect size is arbitrary, and there is no universally agreed upon way to weigh the risk. It has not been determined if the statistically most accurate method for combining results is the fixed, random or quality effect models.[citation needed]

Agenda-driven bias

The most severe fault in meta-analysis[21] often occurs when the person or persons doing the meta-analysis have an economic, social, or political agenda such as the passage or defeat of legislation. People with these types of agendas may be more likely to abuse meta-analysis due to personal bias. For example, researchers favorable to the author's agenda are likely to have their studies cherry-picked while those not favorable will be ignored or labeled as "not credible". In addition, the favored authors may themselves be biased or paid to produce results that support their overall political, social, or economic goals in ways such as selecting small favorable data sets and not incorporating larger unfavorable data sets. The influence of such biases on the results of a meta-analysis is possible because the methodology of meta-analysis is highly malleable.[20]

A 2011 study done to disclose possible conflicts of interests in underlying research studies used for medical meta-analyses reviewed 29 meta-analyses and found that conflicts of interests in the studies underlying the meta-analyses were rarely disclosed. The 29 meta-analyses included 11 from general medicine journals, 15 from specialty medicine journals, and three from the Cochrane Database of Systematic Reviews. The 29 meta-analyses reviewed a total of 509 randomized controlled trials (RCTs). Of these, 318 RCTs reported funding sources, with 219 (69%) receiving funding from industry. Of the 509 RCTs, 132 reported author conflict of interest disclosures, with 91 studies (69%) disclosing one or more authors having industry financial ties. The information was, however, seldom reflected in the meta-analyses. Only two (7%) reported RCT funding sources and none reported RCT author-industry ties. The authors concluded “without acknowledgment of COI due to industry funding or author industry financial ties from RCTs included in meta-analyses, readers’ understanding and appraisal of the evidence from the meta-analysis may be compromised.”[22]

Steps in a meta-analysis

1. Formulation of the problem

2. Search of literature

3. Selection of studies ('incorporation criteria')

  • Based on quality criteria, e.g. the requirement of randomization and blinding in a clinical trial
  • Selection of specific studies on a well-specified subject, e.g. the treatment of breast cancer.
  • Decide whether unpublished studies are included to avoid publication bias (file drawer problem)

4. Decide which dependent variables or summary measures are allowed. For instance:

  • Differences (discrete data)
  • Means (continuous data)
  • Hedges' g is a popular summary measure for continuous data that is standardized in order to eliminate scale differences, but it incorporates an index of variation between groups:
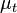\delta ={\frac {\mu _{t}-\mu _{c}}{\sigma }}, in which \mu _{t} is the treatment mean, 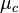\mu _{c} is the control mean, \sigma ^{2} the pooled variance.

5. Model selection (see next paragraph)

For reporting guidelines, see the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) statement [23]

Meta-analysis: methods and assumptions

1. Approaches

In general, two types of evidence can be distinguished when performing a meta-analysis: Individual Participant Data (IPD) and Aggregate Data (AD). Whereas IPD represents raw data as collected by the study centers, AD is more commonly available (e.g. from the literature) and typically represents summary estimates such as odds ratios or relative risks. This distinction has raised the needs for different meta-analytic methods when evidence synthesis is desired, and has led to the development of one-stage and two-stage methods. In one-stage methods the IPD from all studies are modeled simultaneously whilst accounting for the clustering of participants within studies. Conversely, two-stage methods synthesize the AD from each study and hereto consider study weights. By reducing IPD to AD, two-stage methods can also be applied when IPD is available; this makes them an appealing choice when performing a meta-analysis. Although it is conventionally believed that one-stage and two-stage methods yield similar results, recent studies have shown that they may occasionally lead to different conclusions.[24]

2. Statistical Models

Fixed effects model

The fixed effect model provides a weighted average of a series of study estimates. The inverse of the estimates' variance is commonly used as study weight, such that larger studies tend to contribute more than smaller studies to the weighted average. Consequently, when studies within a meta-analysis are dominated by a very large study, the findings from smaller studies are practically ignored.[25] Most importantly, the fixed effects model assumes that all included studies investigate the same population, use the same variable and outcome definitions, etc. This assumption is typically unrealistic as research is often prone to several sources of heterogeneity; e.g. treatment effects may differ according to locale, dosage levels, study conditions, ...

Random effects model

A common model used to synthesize heterogenous research is the random effects model of meta-analysis. This is simply the weighted average of the effect sizes of a group of studies. The weight that is applied in this process of weighted averaging with a random effects meta-analysis is achieved in two steps:[26]

  1. Step 1: inverse variance weighting
  2. Step 2: Un-weighting of this inverse variance weighting by applying a random effects variance component (REVC) that is simply derived from the extent of variability of the effect sizes of the underlying studies.

This means that the greater this variability in effect sizes (otherwise known as heterogeneity), the greater the un-weighting and this can reach a point when the random effects meta-analysis result becomes simply the un-weighted average effect size across the studies. At the other extreme, when all effect sizes are similar (or variability does not exceed sampling error), no REVC is applied and the random effects meta-analysis defaults to simply a fixed effect meta-analysis (only inverse variance weighting).

The extent of this reversal is solely dependent on two factors:[27]

  1. Heterogeneity of precision
  2. Heterogeneity of effect size

The most widely used method to estimate and account for heterogeneity is the DerSimonian-Laird (DL) approach.[28] More recently the iterative and computationally intensive restricted maximum likelihood (REML) approach emerged and is catching up. However, a comparison between these two (and more) models demonstrated that there is little to gain and DL is quite adequate in most scenarios.[29]

However, most meta-analyses include between 2-4 studies and such a sample is more often than not inadequate to accurately estimate heterogeneity. Thus it appears that in small meta-analyses, an incorrect zero between study variance estimate is obtained, leading to a false homogeneity assumption. Overall, it appears that heterogeneity is being consistently underestimated in meta-analyses.[30]

Quality effects model

Doi and Thalib originally introduced the quality effects model [Ref; Doi SA, Thalib L: A quality-effects model for meta-analysis. Epidemiology. 19(1):94-100, 2008] They [31] introduce a new approach to adjustment for inter-study variability by incorporating a relevant component (quality) that differs between studies in addition to the weight based on the intra-study differences that is used in any fixed effects meta-analysis model. The strength of the quality effects meta-analysis is that it allows available methodological evidence to be used over subjective random probability, and thereby helps to close the damaging gap which has opened up between methodology and statistics in clinical research. To do this a correction for the quality adjusted weight of the ith study called taui is introduced.[32] This is a composite based on the quality of other studies except the study under consideration and is utilized to re-distribute quality adjusted weights based on the quality adjusted weights of other studies. In other words, if study i is of good quality and other studies are of poor quality, a proportion of their quality adjusted weights is mathematically redistributed to study i giving it more weight towards the overall effect size. As studies increase in quality, re-distribution becomes progressively less and ceases when all studies are of perfect quality. This model thus replaces the untenable interpretations that abound in the literature and a software is available to explore this method further [33]

Meta-Regression

Main article: Meta-regression

Meta-regression is a tool used in meta-analysis to examine the impact of moderator variables on study effect size using regression-based techniques. Meta-regression is more effective at this task than are standard regression techniques.

Applications in modern science

Modern statistical meta-analysis does more than just combine the effect sizes of a set of studies. It can test if the outcomes of studies show more variation than the variation that is expected because of sampling different research participants. If that is the case, study characteristics such as measurement instrument used, population sampled, or aspects of the studies' design are coded. These characteristics are then used as predictor variables to analyze the excess variation in the effect sizes. Some methodological weaknesses in studies can be corrected statistically. For example, it is possible to correct effect sizes or correlations for the downward bias due to measurement error or restriction on score ranges. Another example is the development of clinical prediction models, where meta-analysis may be used to combine data from different research centers,[34] or even to aggregate existing prediction models.[35]

Meta-analysis can be done with single-subject design as well as group research designs. This is important because much of the research on low incidents populations has been done with single-subject research designs. Considerable dispute exists for the most appropriate meta-analytic technique for single subject research.[36]

Meta-analysis leads to a shift of emphasis from single studies to multiple studies. It emphasizes the practical importance of the effect size instead of the statistical significance of individual studies. This shift in thinking has been termed "meta-analytic thinking". The results of a meta-analysis are often shown in a forest plot.

Results from studies are combined using different approaches. One approach frequently used in meta-analysis in health care research is termed 'inverse variance method'. The average effect size across all studies is computed as a weighted mean, whereby the weights are equal to the inverse variance of each studies' effect estimator. Larger studies and studies with less random variation are given greater weight than smaller studies. Other common approaches include the Mantel–Haenszel method[37] and the Peto method.[citation needed]

A recent approach to studying the influence that weighting schemes can have on results has been proposed through the construct of gravity, which is a special case of combinatorial meta-analysis.

Signed differential mapping is a statistical technique for meta-analyzing studies on differences in brain activity or structure which used neuroimaging techniques such as fMRI, VBM or PET.

Different high throughput techniques such as microarrays have been used to understand Gene expression. MicroRNA expression profiles have been used to identify differentially expressed microRNAs in particular cell or tissue type or disease conditions or to check the effect of a treatment. A meta-analysis of such expression profiles was performed to derive novel conclusions and to validate the known findings.[38]

See also

References

  1. ↑ Greenland S, O' Rourke K: Meta-Analysis. Page 652 in Modern Epidemiology, 3rd ed. Edited by Rothman KJ, Greenland S, Lash T. Lippincott Williams and Wilkins; 2008.
  2. ↑ Glossary at Cochrane Collaboration
  3. ↑ Nordmann, AJ; Kasenda, B; Briel, M (Mar 9, 2012). "Meta-analyses: what they can and cannot do". Swiss medical weekly 142: w13518. doi:10.4414/smw.2012.13518. PMID 22407741. 
  4. ↑ O'Rourke, Keith (2007-12-01). "An historical perspective on meta-analysis: dealing quantitatively with varying study results". J R Soc Med 100 (12): 579–582. doi:10.1258/jrsm.100.12.579. PMC 2121629. PMID 18065712. Retrieved 2009-09-10. 
  5. ↑ Bösch, H. (2004). Reanalyzing a meta-analysis on extra-sensory perception dating from 1940, the first comprehensive meta-analysis in the history of science. In S. Schmidt (Ed.), Proceedings of the 47th Annual Convention of the Parapsychological Association, University of Vienna, (pp. 1–13)
  6. ↑ Glass G. V (1976). "Primary, secondary, and meta-analysis of research". Educational Researcher 5 (10): 3–8. doi:10.3102/0013189X005010003. 
  7. ↑ Cochran WG. Problems Arising in the Analysis of a Series of Similar Experiments. Journal of the Royal Statistical Society, 4:102-118, 1937
  8. ↑ Cochran WG and Carroll SP. A Sampling Investigation of the Efficiency of Weighting Inversely as the Estimated Variance. Biometrics 9:447-459, 1953
  9. ↑ Lelorier, J.; Grégoire, G. V.; Benhaddad, A.; Lapierre, J.; Derderian, F. O. (1997). "Discrepancies between Meta-Analyses and Subsequent Large Randomized, Controlled Trials". New England Journal of Medicine 337 (8): 536–542. doi:10.1056/NEJM199708213370806. PMID 9262498. 
  10. ↑ 10.0 10.1 Slavin, R. E. (1986). "Best-Evidence Synthesis: An Alternative to Meta-Analytic and Traditional Reviews". Educational Researcher 15 (9): 5–9. doi:10.3102/0013189X015009005. 
  11. ↑ Hunter, Schmidt, & Jackson, John E. (1982). Meta-analysis: Cumulating research findings across studies. Beverly Hills, California: Sage. 
  12. ↑ Glass, McGaw, & Smith (1981). Meta-analysis in social research. Beverly Hills, CA: Sage. 
  13. ↑ 13.0 13.1 Rosenthal, Robert (1979). "The "File Drawer Problem" and the Tolerance for Null Results". Psychological Bulletin 86 (3): 638–641. doi:10.1037/0033-2909.86.3.638. 
  14. ↑ Hunter, John E; Schmidt, Frank L (1990). Methods of Meta-Analysis: Correcting Error and Bias in Research Findings. Newbury Park, California; London; New Delhi: SAGE Publications. 
  15. ↑ Light & Pillemer (1984). Summing up: The science of reviewing research. Cambridge, CA: Harvard University Pree. 
  16. ↑ Ioannidis, J., & Trikalinos, T. (2007). "The appropriateness of asymmetry tests for publication bias in meta-analyses: a large survey". Canadian Medical Association Journal 176 (8): 638–641. doi:10.1503/cmaj.060410 
  17. ↑ 17.0 17.1 Ferguson, C., & Brannick, M. (2012). "Publication bias in psychological science: Prevalence, methods for identifying and controlling, and implications for the use of meta-analyses". Psychological Methods 17 (1): 120–128. doi:10.1037/a0024445 
  18. ↑ Simmons, J., Nelson, L & Simonsohn, U. (2011). "False-Positive Psychology : Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant". Psychological Science 22 (11): 1359–1366. doi:10.1177/0956797611417632. PMID 22006061 
  19. ↑ LeBel, E. & Peters, K. (2011). "Fearing the future of empirical psychology: Bem's (2011) evidence of psi as a case study of deficiencies in modal research practice". Review of General Psychology 15 (4): 371–379. doi:10.1037/a0025172 
  20. ↑ 20.0 20.1 Stegenga, J. (2011). "Is meta-analysis the platinum standard?". Studies in History and Philosophy of Biological and Biomedical Sciences 42 (4): 497–507. doi:10.1016/j.shpsc.2011.07.003. 
  21. ↑ H. Sabhan
  22. ↑ "How Well Do Meta-Analyses Disclose Conflicts of Interests in Underlying Research Studies | The Cochrane Collaboration". Cochrane.org. Retrieved 2012-01-13. 
  23. ↑ "The PRISMA statement". Prisma-statement.org. 2012-02-02. Retrieved 2012-02-02. 
  24. ↑ Debray, Thomas P. A.; Moons, K.G.M.; Abdallah, A.Z.; Koffijberg, H.; Riley, R.D. (2013). "Individual participant data meta-analysis for a binary outcome: one-stage or two-stage?". PLoS ONE. 
  25. ↑ Helfenstein U. Data and models determine treatment proposals—an illustration from meta-analysis" Postgrad Med J 2002 Mar;78(917) 131–4
  26. ↑ Senn S. Trying to be precise about vagueness. Stat Med 2007; 26:1417–30
  27. ↑ Al Khalaf MM, Thalib L, Doi SA. "Combining heterogenous studies using the random-effects model is a mistake and leads to inconclusive meta-analyses". Journal of Clinical Epidemiology 2011; 64:119–23
  28. ↑ DerSimonian R, Laird N. (1986) "Meta-analysis in clinical trials". Controlled Clinical Trials, 7, 177–188. doi:10.1016/0197-2456(86)90046-2
  29. ↑ Kontopantelis, E.; Reeves, D. (2010). "Performance of statistical methods for meta-analysis when true study effects are non-normally distributed: A simulation study". Statistical Methods in Medical Research 21 (4): 409–426. doi:10.1177/0962280210392008. PMID 21148194. 
  30. ↑ Kontopantelis, E.; Springate, D. A.; Reeves, D. (2013). "A Re-Analysis of the Cochrane Library Data: The Dangers of Unobserved Heterogeneity in Meta-Analyses". In Friede, Tim. PLoS ONE 8 (7): e69930. doi:10.1371/journal.pone.0069930. PMC 3724681. PMID 23922860. 
  31. ↑ Doi SA, Barendregt JJ, Mozurkewich EL. Meta-analysis of heterogeneous clinical trials: an empirical example. Contemp Clin Trials. 2011 Mar;32(2) 288–98
  32. ↑ Doi SA, Thalib L. A quality-effects model for meta-analysis" Epidemiology 2008 Jan;19(1) 94–100
  33. ↑ MetaXL software page
  34. ↑ Debray, Thomas P. A.; Moons, K. G.; Ahmed, Ikhlaaq; Koffijberg, Hendrik; Riley, Richard D. (2013). "A framework for developing, implementing, and evaluating clinical prediction models in an individual participant data meta-analysis". Statistics in Medicine 32 (18): 3158–80. doi:10.1002/sim.5732. PMID 23307585. 
  35. ↑ Debray, Thomas P. A.; Koffijberg, H; Vergouwe, Y.; Moons, K. G.; Steyerberg, E. W. (2012). "Aggregating published prediction models with individual participant data: a comparison of different approaches". Statistics in Medicine 31 (23): 2697–2712. doi:10.1002/sim.5412. PMID 22733546. 
  36. ↑ Van den Noortgate, W. & Onghena, P. (2007). Aggregating Single-Case Results. The Behavior Analyst Today, 8(2), 196–209 BAO
  37. ↑ Mantel, N.; Haenszel, W. (1959). "Statistical aspects of the analysis of data from the retrospective analysis of disease". Journal of the National Cancer Institute 22 (4): 719–748. PMID 13655060. 
  38. ↑ Bargaje, R., Hariharan, M., Scaria, V., and Pillai, B. (2010) Consensus miRNA expression profiles derived from inter-platform normalization of microarray data. RNA 16(1): 16-25 Bargaje, R; Hariharan, M; Scaria, V; Pillai, B (2010). "Consensus miRNA expression profiles derived from interplatform normalization of microarray data". RNA 16 (1): 16–25. doi:10.1261/rna.1688110. PMC 2802026. PMID 19948767. 
  • Cooper, H. & Hedges, L.V. (1994). The Handbook of Research Synthesis. New York: Russell Sage.
  • Cornell, J. E. & Mulrow, C. D. (1999). Meta-analysis. In: H. J. Adèr & G. J. Mellenbergh (Eds). Research Methodology in the social, behavioral and life sciences (pp. 285–323). London: Sage.
  • Norman S.-L. T. (1999). "Tutorial in Biostatistics. Meta-Analysis: Formulating, Evaluating, Combining, and Reporting". Statistics in Medicine 18 (3): 321–359. doi:10.1002/(SICI)1097-0258(19990215)18:3<321::AID-SIM28>3.0.CO;2-P. PMID 10070677. 
  • Sutton, A.J., Jones, D.R., Abrams, K.R., Sheldon, T.A., & Song, F. (2000). Methods for Meta-analysis in Medical Research. London: John Wiley. ISBN 0-471-49066-0
  • Higgins JPT, Green S (editors). Cochrane Handbook for Systematic Reviews of Interventions Version 5.0.1 [updated September 2008]. The Cochrane Collaboration, 2008. Available from www.cochrane-handbook.org

Further reading

  • Thompson, Simon G; Pocock, Stuart J (2 November 1991). "Can meta-analysis be trusted?". The Lancet 338 (8775): 1127–1130. doi:10.1016/0140-6736(91)91975-Z. PMID 1682553. Retrieved 17 June 2011 . Explores two contrasting views: does meta-analysis provide "objective, quantitative methods for combining evidence from separate but similar studies" or merely "statistical tricks which make unjustified assumptions in producing oversimplified generalisations out of a complex of disparate studies"?
  • Wilson, D. B., & Lipsey, M. W. (2001). Practical meta-analysis. Thousand Oaks: Sage publications. ISBN 0-7619-2168-0
  • O'Rourke, K. (2007) Just the history from the combining of information: investigating and synthesizing what is possibly common in clinical observations or studies via likelihood. Oxford: University of Oxford, Department of Statistics. Gives technical background material and details on the "An historical perspective on meta-analysis" paper cited in the references.
  • Owen, A. B. (2009). "Karl Pearson's meta-analysis revisited". Annals of Statistics, 37 (6B), 3867–3892. Supplementary report.
  • Ellis, Paul D. (2010). The Essential Guide to Effect Sizes: An Introduction to Statistical Power, Meta-Analysis and the Interpretation of Research Results. United Kingdom: Cambridge University Press. ISBN 0-521-14246-6
  • Bonett, D. G. and Price, R. M. (2013), Meta-analysis methods for risk differences. British Journal of Mathematical and Statistical Psychology. doi: 10.1111/bmsp.12024
  • Bonett, D.G. (2012). Replication-extension studies, Current Directions in Psychology, 21, 409-412.
  • Bonett, D.G. (2010). Varying coefficient meta-analysis methods for alpha reliability, Psychological Methods, 15, 368–385.
  • Bonett, D.G. (2009). Meta-analytic interval estimation for standardized and unstandardized mean differences, Psychological Methods, 14, 225–238.
  • Bonett, D.G. (2008). Meta-analytic interval estimation for bivariate correlations, Psychological Methods, 13, 173–189.
  • Stegenga, Jacob (2011). "Is meta-analysis the platinum standard of evidence?". Studies in History and Philosophy of Biological and Biomedical Sciences 42 (4): 497–507. doi:10.1016/j.shpsc.2011.07.003. 

External links

Wikiversity has learning materials about Meta-analysis

Software

 
Statistical theory
Frequentist inference
Specific tests
Bayesian inference
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.