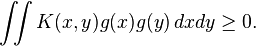Mercer's condition
From Wikipedia, the free encyclopedia
In mathematics, a real-valued function K(x,y) is said to fulfill Mercer's condition if for all square integrable functions g(x) one has
Examples
The constant function
satisfies Mercer's condition, as then the integral becomes by Fubini's theorem
which is indeed non-negative.
See also
- Definite bilinear form
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.