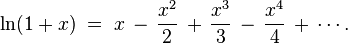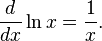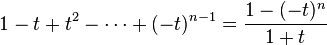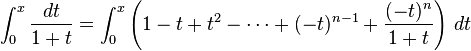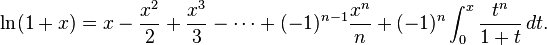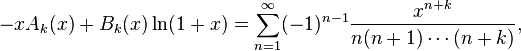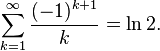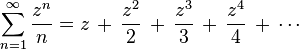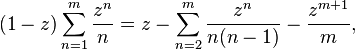Mercator series

From Wikipedia, the free encyclopedia

In mathematics, the Mercator series or Newton–Mercator series is the Taylor series for the natural logarithm:

$\ln(1+x)\;=\;x\,-\,{\frac {x^{2}}{2}}\,+\,{\frac {x^{3}}{3}}\,-\,{\frac {x^{4}}{4}}\,+\,\cdots .$

In summation notation,

$\ln(1+x)\;=\;\sum _{{n=1}}^{\infty }{\frac {(-1)^{{n+1}}}{n}}x^{n}.$

The series converges to the natural logarithm (shifted by 1) whenever −1 < x ≤ 1.

History

The series was discovered independently by Nicholas Mercator, Isaac Newton and Gregory Saint-Vincent. It was first published by Mercator, in his 1668 treatise Logarithmotechnia.

Derivation

The series can be obtained from Taylor's theorem, by inductively computing the n^th derivative of ln x at x = 1, starting with

${\frac {d}{dx}}\ln x={\frac {1}{x}}.$

Alternatively, one can start with the finite geometric series (t ≠ −1)

$1-t+t^{2}-\cdots +(-t)^{{n-1}}={\frac {1-(-t)^{n}}{1+t}}$

which gives

${\frac {1}{1+t}}=1-t+t^{2}-\cdots +(-t)^{{n-1}}+{\frac {(-t)^{n}}{1+t}}.$

It follows that

$\int _{0}^{x}{\frac {dt}{1+t}}=\int _{0}^{x}\left(1-t+t^{2}-\cdots +(-t)^{{n-1}}+{\frac {(-t)^{n}}{1+t}}\right)\,dt$

and by termwise integration,

$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +(-1)^{{n-1}}{\frac {x^{n}}{n}}+(-1)^{n}\int _{0}^{x}{\frac {t^{n}}{1+t}}\,dt.$

If −1 < x ≤ 1, the remainder term tends to 0 as $n\to \infty$ .

This expression may be integrated iteratively k more times to yield

$-xA_{k}(x)+B_{k}(x)\ln(1+x)=\sum _{{n=1}}^{\infty }(-1)^{{n-1}}{\frac {x^{{n+k}}}{n(n+1)\cdots (n+k)}},$

where

$A_{k}(x)={\frac {1}{k!}}\sum _{{m=0}}^{k}{k \choose m}x^{m}\sum _{{l=1}}^{{k-m}}{\frac {(-x)^{{l-1}}}{l}}$

and

$B_{k}(x)={\frac {1}{k!}}(1+x)^{k}$

are polynomials in x.^[1]

Special cases

Setting x = 1 in the Mercator series yields the alternating harmonic series

$\sum _{{k=1}}^{\infty }{\frac {(-1)^{{k+1}}}{k}}=\ln 2.$

Complex series

The complex power series

$\sum _{{n=1}}^{\infty }{\frac {z^{n}}{n}}=z\,+\,{\frac {z^{2}}{2}}\,+\,{\frac {z^{3}}{3}}\,+\,{\frac {z^{4}}{4}}\,+\,\cdots$

is the Taylor series for -log(1 - z), where log denotes the principal branch of the complex logarithm. This series converges precisely for all complex number |z| ≤ 1, z ≠ 1. In fact, as seen by the ratio test, it has radius of convergence equal to 1, therefore converges absolutely on every disk B(0, r) with radius r < 1. Moreover, it converges uniformly on every nibbled disk 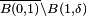$\scriptstyle \overline {B(0,1)}\setminus B(1,\delta )$ , with δ > 0. This follows at once from the algebraic identity:

$(1-z)\sum _{{n=1}}^{m}{\frac {z^{n}}{n}}=z-\sum _{{n=2}}^{m}{\frac {z^{n}}{n(n-1)}}-{\frac {z^{{m+1}}}{m}},$

observing that the right-hand side is uniformly convergent on the whole closed unit disk.

References

↑ Medina, Luis A.; Moll, Victor H.; Rowland, Eric S. (2009). "Iterated primitives of logarithmic powers". arXiv:0911.1325.

Weisstein, Eric W., "Mercator Series", MathWorld.
Eriksson, Larsson & Wahde. Matematisk analys med tillämpningar, part 3. Gothenburg 2002. p. 10.
Some Contemporaries of Descartes, Fermat, Pascal and Huygens from A Short Account of the History of Mathematics (4th edition, 1908) by W. W. Rouse Ball

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.