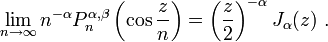Mehler–Heine formula
In mathematics, the Mehler–Heine formula introduced by Mehler (1868) and Heine (1861) describes the asymptotic behavior of the Legendre polynomials as the index tends to infinity, near the edges of the support of the weight. There are generalizations to other classical orthogonal polynomials, which are also called the Mehler–Heine formula. The formula complements the Darboux formulae which describe the asymptotics in the interior and outside the support.
Legendre polynomials
The simplest case of the Mehler–Heine formula states that
where Pn is the Legendre polynomial of order n, and J0 a Bessel function. The limit is uniform over z in an arbitrary bounded domain in the complex plane.
Jacobi polynomials
The generalization to Jacobi polynomials Pα,β
n is given by (Szegő 1939, 8.1) as follows:
References
- Heine, E. (1861), Handbuch der Kugelfunktionen. Theorie und Anwendung. Neudruck. (in German), Georg Reimer, Berlin, Zbl 0103.29304
- Mehler, F. G. (1868), "Ueber die Vertheilung der statischen Elektricität in einem von zwei Kugelkalotten begrenzten Körper.", Journal für Reine und Angewandte Mathematik (in German) 68: 134–150, doi:10.1515/crll.1868.68.134, ISSN 0075-4102
- Szegő, Gábor (1939), Orthogonal Polynomials, Colloquium Publications, XXIII, American Mathematical Society, ISBN 978-0-8218-1023-1, MR 0372517