McGee graph
| McGee Graph | |
|---|---|
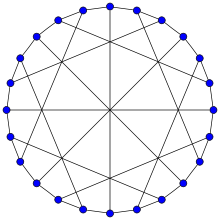 The McGee Graph | |
| Named after | W. F. McGee |
| Vertices | 24 |
| Edges | 36 |
| Radius | 4 |
| Diameter | 4[1] |
| Girth | 7[1] |
| Automorphisms | 32[1] |
| Chromatic number | 3[1] |
| Chromatic index | 3[1] |
| Properties |
Cubic Cage Hamiltonian |
In the mathematical field of graph theory, the McGee Graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.[1]
The McGeeGraph is the unique (3,7)-cage (the smallest cubic graph of girth 7). It is also the smallest cubic cage that is not a Moore graph.
First discovered by Sachs but unpublished,[2] the graph is named after McGee who published the result in 1960.[3] Then, the McGee graph was the proven the unique (3,7)-cage by Tutte in 1966.[4][5][6]
The smallest cubic graphs with crossing numbers 1–8 are known (sequence A110507 in OEIS). The smallest 8-crossing graph is the McGee graph. There exists 5 non-isomorphic cubic graphs of order 24 with crossing number 8.[7] One of them is the generalized Petersen graph G(12,5), also known as the Nauru graph.[8]
The McGeeGraph has radius 4, diameter 4, chromatic number 3 and chromatic index 3. It is also a 3-vertex-connected and a 3-edge-connected graph.
Algebraic properties
The characteristic polynomial of the McGeeGraph graph is : 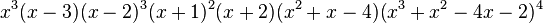 .
.
The automorphism group of the McGee graph is of order 32 and doesn't acts transitively upon its vertices: there are two vertex orbits of lengths 8 and 16. The McGee is the smallest cubic cage that is not a vertex-transitive graph.[9]
Gallery
-

The crossing number of the McGee graph is 8.
-
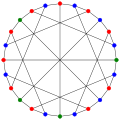
The chromatic number of the McGee graph is 3.
-

The chromatic index of the McGee graph is 3.
-

The acyclic chromatic number of the McGee graph is 3.
-
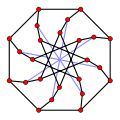
Alternative drawing of the McGee graph.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Weisstein, Eric W., "McGee Graph", MathWorld.
- ↑ Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
- ↑ McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
- ↑ Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
- ↑ Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982
- ↑ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
- ↑ Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009
- ↑ Weisstein, Eric W., "Graph Crossing Number", MathWorld.
- ↑ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.