Maximal arc

From Wikipedia, the free encyclopedia

A Maximal arc in a finite projective plane is a largest possible (k,d)-arc in that projective plane. If the finite projective plane has order q (there are q+1 points on any line), then for a maximal arc, k, the number of points of the arc, is the maximum possible (= qd + d - q) with the property that no d+1 points of the arc lie on the same line.

Definition

Let $\pi$ be a finite projective plane of order q (not necessarily desarguesian). Maximal arcs of degree d ( 2 ≤ d ≤ q- 1) are (k,d)-arcs in $\pi$ , where k is maximal with respect to the parameter d, in other words, k = qd + d - q.

Equivalently, one can define maximal arcs of degree d in $\pi$ as non-empty sets of points K such that every line intersects the set either in 0 or d points.

Some authors permit the degree of a maximal arc to be 1, q or even q+ 1.^[1] Letting K be a maximal (k, d)-arc in a projective plane of order q, if

d = 1, K is a point of the plane,
d = q, K is the complement of a line (an affine plane of order q), and
d = q + 1, K is the entire projective plane.

All of these cases are considered to be trivial examples of maximal arcs, existing in any type of projective plane for any value of q. When 2 ≤ d ≤ q- 1, the maximal arc is called non-trivial, and the definition given above and the properties listed below all refer to non-trivial maximal arcs.

Properties

The number of lines through a fixed point p, not on a maximal arc K, intersecting K in d points, equals 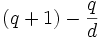$(q+1)-\frac{q}{d}$ . Thus, d divides q.
In the special case of d = 2, maximal arcs are known as hyperovals which can only exist if q is even.
An arc K having one fewer point than a maximal arc can always be uniquely extended to a maximal arc by adding to K the point at which all the lines meeting K in d - 1 points meet.^[2]
In PG(2,q) with q odd, no non-trivial maximal arcs exist.^[3]
In PG(2,2^h), maximal arcs for every degree 2^t, 1 ≤ t ≤ h exist.^[4]

Partial geometries

One can construct partial geometries, derived from maximal arcs:^[5]

Let K be a maximal arc with degree d. Consider the incidence structure $S(K)=(P,B,I)$ , where P contains all points of the projective plane not on K, B contains all line of the projective plane intersecting K in d points, and the incidence I is the natural inclusion. This is a partial geometry : $pg(q-d,q-\frac{q}{d},q-\frac{q}{d}-d+1)$ .
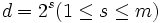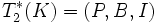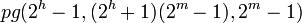Consider the space $PG(3,2^h) (h\geq 1)$ and let K a maximal arc of degree $d=2^s (1\leq s\leq m)$ in a two-dimensional subspace $\pi$ . Consider an incidence structure $T_2^{*}(K)=(P,B,I)$ where P contains all the points not in $\pi$ , B contains all lines not in $\pi$ and intersecting $\pi$ in a point in K, and I is again the natural inclusion. $T_2^{*}(K)$ is again a partial geometry : $pg(2^h-1,(2^h+1)(2^m-1),2^m-1)\,$ .

Notes

↑ Hirschfeld 1979, pp. 325
↑ Hirschfeld 1979, pg. 328
↑ Ball, Blokhuis & Mazzocca 1997
↑ Denniston 1969
↑ Thas 1974

References

Ball, S.; Blokhuis, A.; Mazzocca, F. (1997), "Maximal arcs in Desarguesian planes of odd order do not exist", Combinatorica 17: 31–41, MR 98h:51014, Zbl 0880.51003
Denniston, R.H.F. (1969), "Some maximal arcs in finite projective planes", J. Combin. Theory 6: 317–319, MR 39#1345, Zbl 0167.49106
Hirschfeld, J.W.P. (1979), Projective Geometries over Finite Fields, New York: Oxford University Press, ISBN 0-19-853526-0
Mathon, R. (2002), "New maximal arcs in Desarguesian planes", J. Combin. Theory Ser. A 97: 353–368, MR 2002k:51012, Zbl 01763788
Thas, J.A. (1974), "Construction of maximal arcs and partial geometries", Geom. Dedicata 3: 61–64, MR 50#1931, Zbl 0285.50018

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.