Max–min inequality

From Wikipedia, the free encyclopedia

In mathematics, the max–min inequality is as follows: for any function 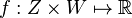f: Z \times W \mapsto \mathbb{R}

\sup_{z \in Z} \inf_{w \in W} f(z, w) \leq \inf_{w \in W} \sup_{z \in Z} f(z, w). \,

When equality holds one says that f, W, Z satisfies the strong max–min property (or the saddle-point property).

Proof

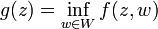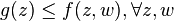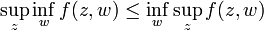Define g(z) = \inf_{w \in W} f(z, w) . Therefore, g(z) \leq f(z, w), \forall z, w , which implies that \sup_z g(z) \leq \sup_z f(z, w) , \forall w . As a result, \sup_z \inf_w f(z,w) \leq \inf_w \sup_z f(z, w) .

References

See also

Min-max theorem

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.