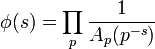Matsumoto zeta function

From Wikipedia, the free encyclopedia

In mathematics, Matsumoto zeta functions are a type of zeta function introduced by Kohji Matsumoto in 1990. They are functions of the form

\phi (s)=\prod _{{p}}{\frac {1}{A_{p}(p^{{-s}})}}

where p is a prime and Ap is a polynomial.

References

  • Matsumoto, Kohji (1990), "Value-distribution of zeta-functions", Analytic number theory ({T}okyo, 1988), Lecture Notes in Math. 1434, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0097134, MR 1071754 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.