Matrix gamma distribution

From Wikipedia, the free encyclopedia

Matrix gamma
Notation	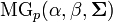${{\rm {MG}}}_{{p}}(\alpha ,\beta ,{\boldsymbol \Sigma })$
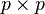Parameters	shape parameter (real) $\beta >0$ scale parameter ${\boldsymbol \Sigma }$ scale (positive-definite real $p\times p$ matrix)
Support	${\mathbf {X}}$ positive-definite real $p\times p$ matrix
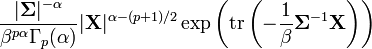
pdf	${\frac {\|{\boldsymbol \Sigma }\|^{{-\alpha }}}{\beta ^{{p\alpha }}\Gamma _{p}(\alpha )}}\|{\mathbf {X}}\|^{{\alpha -(p+1)/2}}\exp \left({{\rm {tr}}}\left(-{\frac {1}{\beta }}{\boldsymbol \Sigma }^{{-1}}{\mathbf {X}}\right)\right)$ $\Gamma _{p}$ is the multivariate gamma function.

In statistics, a matrix gamma distribution is a generalization of the gamma distribution to positive-definite matrices.^[1] It is a more general version of the Wishart distribution, and is used similarly, e.g. as the conjugate prior of the precision matrix of a multivariate normal distribution and matrix normal distribution. The compound distribution resulting from compounding a matrix normal with a matrix gamma prior over the precision matrix is a generalized matrix t-distribution.^{[citation needed]}

This reduces to the Wishart distribution with $\beta =2,\alpha ={\frac {n}{2}}.$

Notes

↑ Iranmanesha, Anis, M. Arashib and S. M. M. Tabatabaeya (2010). "On Conditional Applications of Matrix Variate Normal Distribution". Iranian Journal of Mathematical Sciences and Informatics, 5:2, pp. 33–43.

References

Gupta, A. K.; Nagar, D. K. (1999) Matrix Variate Distributions, Chapman and Hall/CRC ISBN 978-1584880462

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle Xenakis

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Matrix gamma distribution

See also

Notes

References