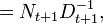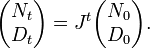Matrix difference equation
A matrix difference equation[1][2] is a difference equation in which the value of a vector (or sometimes, a matrix) of variables at one point in time is related to its own value at one or more previous points in time, using matrices. Occasionally, the time-varying entity may itself be a matrix instead of a vector. The order of the equation is the maximum time gap between any two indicated values of the variable vector. For example,
is an example of a second-order matrix difference equation, in which x is an n × 1 vector of variables and A and B are n×n matrices. This equation is homogeneous because there is no vector constant term added to the end of the equation. The same equation might also be written as
or as
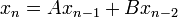 .
.
The most commonly encountered matrix difference equations are first-order.
Non-homogeneous first-order matrix difference equations and the steady state
An example of a non-homogeneous first-order matrix difference equation is
with additive constant vector b. The steady state of this system is a value x* of the vector x which, if reached, would not be deviated from subsequently. x* is found by setting 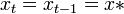 in the difference equation and solving for x* to obtain
in the difference equation and solving for x* to obtain
where  is the n×n identity matrix, and where it is assumed that
is the n×n identity matrix, and where it is assumed that ![[I-A]](/2014-wikipedia_en_all_02_2014/I/media/0/4/9/9/0499dc8d5b79109560ec7ac8ed4ef4d3.png) is invertible. Then the non-homogeneous equation can be rewritten in homogeneous form in terms of deviations from the steady state:
is invertible. Then the non-homogeneous equation can be rewritten in homogeneous form in terms of deviations from the steady state:
Stability of the first-order case
The first-order matrix difference equation [xt - x*] = A[xt-1-x*] is stable -- that is, 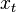 converges asymptotically to the steady state x* -- if and only if all eigenvalues of the transition matrix A (whether real or complex) have an absolute value which is less than 1.
converges asymptotically to the steady state x* -- if and only if all eigenvalues of the transition matrix A (whether real or complex) have an absolute value which is less than 1.
Solution of the first-order case
Assume that the equation has been put in the homogeneous form 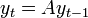 . Then we can iterate and substitute repeatedly from the initial condition
. Then we can iterate and substitute repeatedly from the initial condition  , which is the initial value of the vector y and which must be known in order to find the solution:
, which is the initial value of the vector y and which must be known in order to find the solution:
and so forth. By induction, we obtain the solution in terms of t:
where P is an n × n matrix whose columns are the eigenvectors of A (assuming the eigenvalues are all distinct) and D is an n × n diagonal matrix whose diagonal elements are the eigenvalues of A. This solution motivates the above stability result: 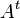 shrinks to the zero matrix over time if and only if the eigenvalues of A are all less than unity in absolute value.
shrinks to the zero matrix over time if and only if the eigenvalues of A are all less than unity in absolute value.
Extracting the dynamics of a single scalar variable from a first-order matrix system
Starting from the n-dimensional system 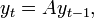 we can extract the dynamics of one of the state variables, say
we can extract the dynamics of one of the state variables, say  The above solution equation for
The above solution equation for 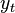 shows that the solution for
shows that the solution for  is in terms of the n eigenvalues of A. Therefore the equation describing the evolution of
is in terms of the n eigenvalues of A. Therefore the equation describing the evolution of  by itself must have a solution involving those same eigenvalues. This description intuitively motivates the equation of evolution of
by itself must have a solution involving those same eigenvalues. This description intuitively motivates the equation of evolution of 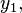 which is
which is
where the parameters  are from the characteristic equation of the matrix A:
are from the characteristic equation of the matrix A:
Thus each individual scalar variable of an n-dimensional first-order linear system evolves according to a univariate nth degree difference equation, which has the same stability property (stable or unstable) as does the matrix difference equation.
Solution and stability of higher-order cases
Matrix difference equations of higher order—that is, with a time lag longer than one period—can be solved, and their stability analyzed, by converting them into first-order form using a block matrix. For example, suppose we have the second-order equation
with the variable vector x being n×1 and A and B being n×n. This can be stacked in the form
where  is the n×n identity matrix and 0 is the n×n zero matrix. Then denoting the 2n×1 stacked vector of current and once-lagged variables as
is the n×n identity matrix and 0 is the n×n zero matrix. Then denoting the 2n×1 stacked vector of current and once-lagged variables as 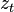 and the 2n×2n block matrix as L, we have as before the solution
and the 2n×2n block matrix as L, we have as before the solution
Also as before, this stacked equation and thus the original second-order equation are stable if and only if all eigenvalues of the matrix L are smaller than unity in absolute value.
Nonlinear matrix difference equations: Riccati equations
In linear-quadratic-Gaussian control, there arises a nonlinear matrix equation for the evolution backwards through time of a current-and-future-cost matrix, denoted below as H. This equation is called a discrete dynamic Riccati equation, and it arises when a variable vector evolving according to a linear matrix difference equation is to be controlled by manipulating an exogenous vector in order to optimize a quadratic cost function. This Riccati equation assumes the following form or a similar form:
where H, K, and A are n×n, C is n×k, R is k×k, n is the number of elements in the vector to be controlled, and k is the number of elements in the control vector. The parameter matrices A and C are from the linear equation, and the parameter matrices K and R are from the quadratic cost function.
In general this equation cannot be solved analytically for  in terms of t ; rather, the sequence of values for
in terms of t ; rather, the sequence of values for  is found by iterating the Riccati equation. However, it was shown in [3] that this Riccati equation can be solved analytically if R is the zero matrix and n=k+1, by reducing it to a scalar rational difference equation; moreover, for any k and n if the transition matrix A is nonsingular then the Riccati equation can be solved analytically in terms of the eigenvalues of a matrix, although these may need to be found numerically.[4]
is found by iterating the Riccati equation. However, it was shown in [3] that this Riccati equation can be solved analytically if R is the zero matrix and n=k+1, by reducing it to a scalar rational difference equation; moreover, for any k and n if the transition matrix A is nonsingular then the Riccati equation can be solved analytically in terms of the eigenvalues of a matrix, although these may need to be found numerically.[4]
In most contexts the evolution of H backwards through time is stable, meaning that H converges to a particular fixed matrix H* which may be irrational even if all the other matrices are rational.
A related Riccati equation[5] is
in which the matrices X, A, B, C, and E are all n×n. This equation can be solved explicitly. Suppose 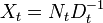 , which certainly holds for t=0 with N0 = X0 and with D0 equal to the identity matrix. Then using this in the difference equation yields
, which certainly holds for t=0 with N0 = X0 and with D0 equal to the identity matrix. Then using this in the difference equation yields
so by induction the form 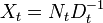 holds for all t. Then the evolution of N and D can be written as
holds for all t. Then the evolution of N and D can be written as
Thus
References
- ↑ Cull, Paul; Flahive, Mary; and Robson, Robbie. Difference Equations: From Rabbits to Chaos, Springer, 2005, chapter 7; ISBN 0-387-23234-6.
- ↑ Chiang, Alpha C., Fundamental Methods of Mathematical Economics, third edition, McGraw-Hill, 1984: 608–612.
- ↑ Balvers, Ronald J., and Mitchell, Douglas W., "Reducing the dimensionality of linear quadratic control problems," Journal of Economic Dynamics and Control 31, 2007, 141–159.
- ↑ Vaughan, D. R., "A nonrecursive algebraic solution for the discrete Riccati equation," IEEE Transactions on Automatic Control 15, 1970, 597-599.
- ↑ Martin, C. F., and Ammar, G., "The geometry of the matrix Riccati equation and associated eigenvalue method," in Bittani, Laub, and Willems (eds.), The Riccati Equation, Springer-Verlag, 1991.
See also
- Matrix differential equation
- Difference equation
- Dynamical system
- Matrix Riccati equation#Mathematical description of the problem and solution
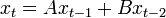
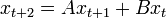

![x^{{*}}=[I-A]^{{-1}}b\,](/2014-wikipedia_en_all_02_2014/I/media/2/7/0/7/27075c148ad63a4415f15d9496a8a8ff.png)
![[x_{t}-x^{{*}}]=A[x_{{t-1}}-x^{{*}}].\,](/2014-wikipedia_en_all_02_2014/I/media/c/0/1/f/c01f8d8f1cc4e01625eb4596d2773395.png)
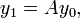
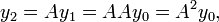
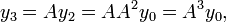

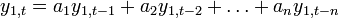
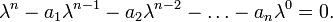


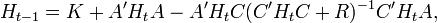

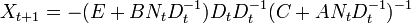
![=-(ED_{t}+BN_{t})[(C+AN_{t}D_{t}^{{-1}})D_{t}]^{{-1}}](/2014-wikipedia_en_all_02_2014/I/media/8/5/3/d/853d3a6d7b490c12466ab90fc34aaac9.png)
![=-(ED_{t}+BN_{t})[CD_{t}+AN_{t}]^{{-1}}](/2014-wikipedia_en_all_02_2014/I/media/1/d/3/c/1d3c8e83c002be70e019033e85b62b27.png)