Markov kernel
From Wikipedia, the free encyclopedia
In probability theory, a Markov kernel (or stochastic kernel) is a map that plays the role, in the general theory of Markov processes, that the transition matrix does in the theory of Markov processes with a finite state space.[1][2]
Formal definition
Let 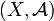 ,
, 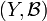 be measurable spaces. A Markov kernel with source
be measurable spaces. A Markov kernel with source 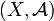 and target
and target 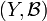 is a map
is a map  that associates to each point
that associates to each point  a probability measure
a probability measure 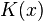 on
on 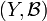 such that, for every measurable set
such that, for every measurable set 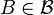 , the map
, the map 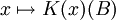 is measurable with respect to the
is measurable with respect to the 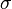 -algebra
-algebra  .
.
Let 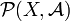 denote the set of all probability measures on the measurable
space
denote the set of all probability measures on the measurable
space 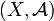 . If
. If  is a Markov kernel with source
is a Markov kernel with source 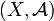 and target
and target 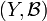 then we can naturally associate to
then we can naturally associate to  a map
a map  defined as follows: given
defined as follows: given  in
in 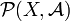 , we set
, we set 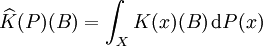 , for all
, for all  in
in 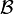 .
.
Estimation
The kernel can be estimated using kernel density estimation.[3]
References
- ↑ Epstein, P.; Howlett, P.; Schulze, M. S. (2003). "Distribution dynamics: Stratification, polarization, and convergence among OECD economies, 1870–1992". Explorations in Economic History 40: 78. doi:10.1016/S0014-4983(02)00023-2.
- ↑ Reiss, R. D. (1993). A Course on Point Processes. Springer Series in Statistics. doi:10.1007/978-1-4613-9308-5. ISBN 978-1-4613-9310-8.
- ↑ Poletti Laurini, M. R.; Valls Pereira, P. L. (2009). "Conditional stochastic kernel estimation by nonparametric methods". Economics Letters 105 (3): 234. doi:10.1016/j.econlet.2009.08.012.
- Bauer, Heinz (1996), Probability Theory, de Gruyter, ISBN 3-11-013935-9
- §36. Kernels and semigroups of kernels
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.