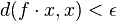Margulis lemma

From Wikipedia, the free encyclopedia

In mathematics, the Margulis lemma (named after Grigory Margulis) is a result about discrete subgroups of isometries of a symmetric space (e.g. the hyperbolic n-space), or more generally a space of non-positive curvature.

Theorem: Let S be a Riemannian symmetric space of non-compact type. There is a positive constant

$\epsilon =\epsilon (S)>0$

with the following property. Let F be subset of isometries of S. Suppose there is a point x in S such that

$d(f\cdot x,x)<\epsilon$

for all f in F. Assume further that the subgroup $\Gamma$ generated by F is discrete in Isom(S). Then $\Gamma$ is virtually nilpotent. More precisely, there exists a subgroup $\Gamma _{0}$ in $\Gamma$ which is nilpotent of nilpotency class at most r and of index at most N in $\Gamma$ , where r and N are constants depending on S only.

The constant 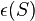$\epsilon (S)$ is often referred as the Margulis constant.

References

Werner Ballman, Mikhael Gromov, Victor Schroeder, Manifolds of Non-positive Curvature, Birkhauser, Boston (1985) p. 107

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.