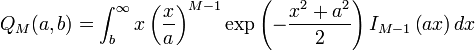Marcum Q-function

From Wikipedia, the free encyclopedia

In statistics, the Marcum-Q-function 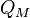$Q_{M}$ is defined as

$Q_{M}(a,b)=\int _{{b}}^{{\infty }}x\left({\frac {x}{a}}\right)^{{M-1}}\exp \left(-{\frac {x^{2}+a^{2}}{2}}\right)I_{{M-1}}\left(ax\right)dx$

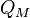$Q_{M}$ is also defined as

$Q_{M}(a,b)=\exp \left(-{\frac {a^{2}+b^{2}}{2}}\right)\sum _{{k=1-M}}^{{\infty }}\left({\frac {a}{b}}\right)^{{k}}I_{{k}}\left(ab\right)$

with modified Bessel function $I_{{M-1}}$ of order M − 1. The Marcum Q-function is used for example as a cumulative distribution function for noncentral chi-squared and Rice distributions.

The Marcum Q-function is monotonic and log-concave.^[1]

References

Marcum, J. I. (1950) "Table of Q Functions". U.S. Air Force RAND Research Memorandum M-339. Santa Monica, CA: Rand Corporation, Jan. 1, 1950.
Nuttall, Albert H. (1975): Some Integrals Involving the Q_M Function, IEEE Transactions on Information Theory, 21(1), 95-96, ISSN 0018-9448
Weisstein, Eric W. Marcum Q-Function. From MathWorld—A Wolfram Web Resource.

↑ Yin Sun, Árpád Baricz, and Shidong Zhou (2010) On the Monotonicity, Log-Concavity, and Tight Bounds of the Generalized Marcum and Nuttall Q-Functions. IEEE Transactions on Information Theory, 56(3), 1166-1186, ISSN 0018-9448

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.