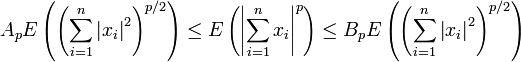Marcinkiewicz–Zygmund inequality

From Wikipedia, the free encyclopedia

In mathematics, the Marcinkiewicz–Zygmund inequality, named after Józef Marcinkiewicz and Antoni Zygmund, gives relations between moments of a collection of independent random variables. It is a generalization of the rule for the sum of variances of independent random variables to moments of arbitrary order.

Statement of the inequality

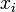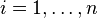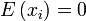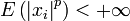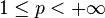Theorem [1][2] If \textstyle x_{{i}}, \textstyle i=1,\ldots ,n, are independent random variables such that \textstyle E\left(x_{{i}}\right)=0 and \textstyle E\left(\left\vert x_{{i}}\right\vert ^{{p}}\right)<+\infty , \textstyle 1\leq p<+\infty ,

A_{{p}}E\left(\left(\sum _{{i=1}}^{{n}}\left\vert x_{{i}}\right\vert ^{{2}}\right)_{{{}}}^{{p/2}}\right)\leq E\left(\left\vert \sum _{{i=1}}^{{n}}x_{{i}}\right\vert ^{{p}}\right)\leq B_{{p}}E\left(\left(\sum _{{i=1}}^{{n}}\left\vert x_{{i}}\right\vert ^{{2}}\right)_{{{}}}^{{p/2}}\right)

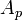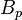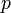where \textstyle A_{{p}} and \textstyle B_{{p}} are positive constants, which depend only on \textstyle p.

The second-order case

In the case 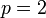\textstyle p=2, the inequality holds with 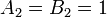\textstyle A_{{2}}=B_{{2}}=1, and it reduces to the rule for the sum of variances of independent random variables with zero mean, known from elementary statistics: If 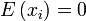\textstyle E\left(x_{{i}}\right)=0 and \textstyle E\left(\left\vert x_{{i}}\right\vert ^{{2}}\right)<+\infty , then

{\mathrm {Var}}\left(\sum _{{i=1}}^{{n}}x_{{i}}\right)=E\left(\left\vert \sum _{{i=1}}^{{n}}x_{{i}}\right\vert ^{{2}}\right)=\sum _{{i=1}}^{{n}}\sum _{{j=1}}^{{n}}E\left(x_{{i}}\overline {x}_{{j}}\right)=\sum _{{i=1}}^{{n}}E\left(\left\vert x_{{i}}\right\vert ^{{2}}\right)=\sum _{{i=1}}^{{n}}{\mathrm {Var}}\left(x_{{i}}\right).

See also

Several similar moment inequalities are known as Khintchine inequality and Rosenthal inequalities, and there are also extensions to more general symmetric statistics of independent random variables.[3]

Notes

  1. ↑ J. Marcinkiewicz and A. Zygmund. Sur les foncions independantes. Fund. Math., 28:60–90, 1937. Reprinted in Józef Marcinkiewicz, Collected papers, edited by Antoni Zygmund, Panstwowe Wydawnictwo Naukowe, Warsaw, 1964, pp. 233–259.
  2. ↑ Yuan Shih Chow and Henry Teicher. Probability theory. Independence, interchangeability, martingales. Springer-Verlag, New York, second edition, 1988.
  3. ↑ R. Ibragimov and Sh. Sharakhmetov. Analogues of Khintchine, Marcinkiewicz–Zygmund and Rosenthal inequalities for symmetric statistics. Scandinavian Journal of Statistics, 26(4):621–633, 1999.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.