Majorana fermion

Standard model of particle physics
Large Hadron Collider tunnel at CERN
Background Particle physics Standard Model Quantum field theory Gauge theory Spontaneous symmetry breaking Higgs mechanism
Constituents Electroweak interaction Quantum chromodynamics CKM matrix
Limitations Strong CP problem Hierarchy problem Neutrino oscillations See also: Physics beyond the Standard Model
Scientists Rutherford · Thomson · Chadwick · Bose · Sudarshan · Koshiba · Davis, Jr. · Anderson · Fermi · Dirac · Feynman · Rubbia · Gell-Mann · Kendall · Taylor · Friedman · Powell · P. W. Anderson · Glashow · Meer · Cowan · Nambu · Chamberlain · Cabibbo · Schwartz · Perl · Majorana · Weinberg · Lee · Ward · Salam · Kobayashi · Maskawa · Yang · Yukawa · 't Hooft · Veltman · Gross · Politzer · Wilczek · Cronin · Fitch · Vleck · Higgs · Englert · Brout · Hagen · Guralnik  · Kibble  · Ting · Richter
v t e

A Majorana fermion, also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles. No elementary fermions are known to be their own antiparticle, though the nature of the neutrino is not settled and it might be a Majorana fermion. By contrast, it is common that bosons are their own antiparticle, such as the photon.

In condensed matter physics, Majorana fermions exist as quasiparticle excitations in superconductors and can be used to form Majorana bound states possessing non-abelian statistics.

Theory

The concept goes back to Ettore Majorana's 1937 suggestion^[1] that neutral spin-1/2 particles can be described by a real wave equation (the Majorana equation), and would therefore be identical to their antiparticle (since the wave function of particle and antiparticle are related by complex conjugation).

The difference between Majorana fermions and Dirac fermions can be expressed mathematically in terms of the creation and annihilation operators of second quantization. The creation operator 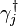creates a fermion in quantum state (described by a real wave function), while the annihilation operator 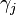annihilates it (or, equivalently, creates the corresponding antiparticle). For a Dirac fermion the operators 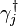and 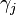are distinct, while for a Majorana fermion they are identical.

Elementary particle

No elementary particle in the Standard Model is known to be a Majorana fermion. However, the nature of the neutrino is not yet definitely settled; it might be a Majorana fermion or it might be a Dirac fermion. Gauge theories suggest that neutrinos are Majorana fermions, so lepton number is violated in nature, which could be verified in both low and high energy experiments. At low energies, neutrinoless double beta decay, where two neutrons decay into two protons and two electrons only, is possible; experiments are underway to search for this type of decay.^[2] The significance of neutrinoless double beta decay stems from the fact that, in any gauge theory like the Standard Model the observation of neutrinoless double beta decay necessarily implies Majorana nature of neutrinos, a result known as the Black Box theorem ^[3]

The high energy analog of the neutrinoless double beta decay process is the production of same sign charged lepton pairs at hadron colliders;^[4] it is being searched for by both the ATLAS and CMS experiments at the Large Hadron Collider. In theories based on left–right symmetry, there is a deep connection between these processes.^[5] In the most accepted explanation of the smallness of neutrino mass, the seesaw mechanism, the neutrino is naturally a Majorana fermion.

Majorana fermions cannot possess intrinsic electric or magnetic moments, only toroidal moments.^[6][7][8] Such minimal interaction with electromagnetic fields makes them potential candidates for cold dark matter.^[9][10] The hypothetical neutralino of supersymmetric models is a Majorana fermion.

Majorana bound states

In superconducting materials, Majorana fermions can emerge as (non-fundamental) quasiparticles. This becomes possible because a quasiparticle in a superconductor is its own antiparticle. Mathematically, the superconductor imposes electron hole "symmetry" on the quasiparticle excitations, relating the creation operator 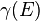at energy to the annihilation operator 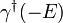at energy 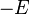. Majorana fermions can be bound to a defect at zero energy, and then the combined objects are called Majorana bound states or Majorana zero modes.^[11] This name is more appropriate than Majorana fermion (although the distinction is not always made in the literature), since the statistics of these objects is no longer fermionic. Instead, the Majorana bound states are an example of non-abelian anyons: interchanging them changes the state of the system in a way which depends only on the order in which exchange was performed. The non-abelian statistics that Majorana bound states possess allows to use them as a building block for a topological quantum computer.^[12]

A quantum vortex in certain superconductors or superfluids can trap midgap states, so this is one source of Majorana bound states.^[13][14][15] Shockley states at the end points of superconducting wires or line defects are an alternative, purely electrical, source.^[16] An altogether different source uses the fractional quantum Hall effect as a substitute for the superconductor.^[17]

Experiments in superconductivity

In 2008 Fu and Kane provided a groundbreaking development by theoretically predicting that Majorana bound states can appear at the interface between topological insulators and superconductors.^[18][19] Many proposals of a similar spirit soon followed, where it was shown that Majorana bound states can appear even without topological insulator. An intense search to provide experimental evidence of Majorana bound states in superconductors^[20][21] first produced some positive results in 2012.^[22][23] A team from the Kavli Institute of Nanoscience at Delft University of Technology in the Netherlands reported an experiment involving indium antimonide nanowires connected to a circuit with a gold contact at one end and a slice of superconductor at the other. When exposed to a moderately strong magnetic field the apparatus showed a peak electrical conductance at zero voltage that is consistent with the formation of a pair of Majorana bound states, one at either end of the region of the nanowire in contact with the superconductor.^[24]

This experiment from Delft marks a possible verification of independent theoretical proposals from two groups^[25][26] predicting the solid state manifestation of Majorana bound states in semiconducting wires.

References

Further reading

• Palash B. Pal: Dirac, Majorana and Weyl fermions, arXiv:1006.1718, 24 June / 17 July 2009 (introductory article)

v t e Particles in physics Elementary Fermions Quarks u u d d c c s s t t b b Leptons e− e+ μ− μ+ τ− τ+ ν e ν e ν μ ν μ ν τ ν τ Bosons Gauge γ g W± · Z Scalar H0 Others Ghosts Hypothetical Superpartners Gauginos Gluino Gravitino Others Axino Chargino Higgsino Neutralino Sfermion Others A0 Dilaton G J Majorana fermion m Tachyon X Y W' Z' Sterile neutrino Composite Hadrons Baryons / Hyperons N p n Δ Λ Σ Ξ Ω Mesons / Quarkonia π ρ η η′ φ ω J/ψ ϒ θ K B D T Others Atomic nuclei Atoms Diquarks Exotic atoms Positronium Muonium Tauonium Onia Superatoms Molecules Hypothetical Exotic hadrons Exotic baryons Dibaryon Pentaquark Skyrmion Exotic mesons Glueball Tetraquark Others Mesonic molecule Pomeron Quasiparticles Davydov soliton Exciton Hole Magnon Phonon Plasmaron Plasmon Polariton Polaron Roton Trion Lists Baryons Mesons Particles Quasiparticles Timeline of particle discoveries Wikipedia books Hadronic Matter Particles of the Standard Model Leptons Quarks Physics portal