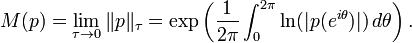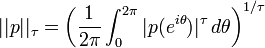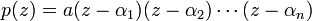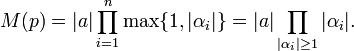Mahler measure
From Wikipedia, the free encyclopedia
In mathematics, the Mahler measure  of a polynomial
of a polynomial ![p(x)\in {\mathbb {C}}[x]](/2014-wikipedia_en_all_02_2014/I/media/7/3/f/2/73f2dfba89af90f12344292294229ec9.png) with complex coefficients is
with complex coefficients is
Here
is the  norm of
norm of  (although this is not a true norm for values of
(although this is not a true norm for values of  ).
).
It can be shown that if
then
The Mahler measure of an algebraic number  is defined as the Mahler measure of the minimal polynomial of
is defined as the Mahler measure of the minimal polynomial of  over
over  .
.
The measure is named after Kurt Mahler.
Properties
- The Mahler measure is multiplicative, i.e.
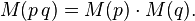
- (Kronecker's Theorem) If
 is an irreducible monic integer polynomial with
is an irreducible monic integer polynomial with 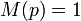 , then either
, then either 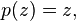 or
or  is a cyclotomic polynomial.
is a cyclotomic polynomial. - Lehmer's conjecture asserts that there is a constant
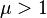 such that if
such that if  is an irreducible integer polynomial, then either
is an irreducible integer polynomial, then either 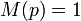 or
or  .
. - The Mahler measure of a monic integer polynomial is a Perron number.
Higher Dimensional Mahler Measure
The Mahler measure  of a multi-variable polynomial
of a multi-variable polynomial ![p(x_{1},\ldots ,x_{n})\in {\mathbb {C}}[x_{1},\ldots ,x_{n}]](/2014-wikipedia_en_all_02_2014/I/media/5/a/f/6/5af6b0299d64309f456ea7d435846b7e.png) is defined similarly by the formula
is defined similarly by the formula
Multi-variable Mahler measures have been shown, in some cases, to be related to special values
of zeta-functions and 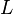 -functions.
-functions.
See also
References
- Hazewinkel, Michiel, ed. (2001), "m120070", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Peter Borwein (2002). Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics. Springer-Verlag. pp. 3, 15. ISBN 0-387-95444-9.
- J.L. Jensen (1899). "Sur un nouvel et important théorème de la théorie des fonctions". Acta Mathematica 22: 359–364. doi:10.1007/BF02417878.
- Knuth, Donald E (1997). "4.6.2 Factorization of Polynomials". Seminumerical Algorithms. The Art of Computer Programming 2 (Third ed.). Reading, Massachusetts: Addison-Wesley. pp. 439–461, 678–691. ISBN 0-201-89684-2.
- M.J. Mossinghoff (1998). "Polynomials with Small Mahler Measure". Mathematics of Computation 67 (224): 1697–1706. doi:10.1090/S0025-5718-98-01006-0.
- Smyth, Chris (2008). "The Mahler measure of algebraic numbers: a survey". In McKee, James; Smyth, Chris. Number Theory and Polynomials. London Mathematical Society Lecture Note Series 352. Cambridge University Press. pp. 322–349. ISBN 978-0-521-71467-9.
External links
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.