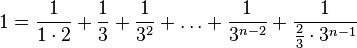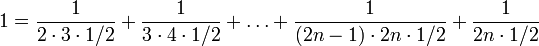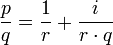Mahāvīra (mathematician)

From Wikipedia, the free encyclopedia

Mahāvīra (or Mahaviracharya, "Mahavira the Teacher") was a 9th-century Jain mathematician from Mysore, India.^[1]^[2]^[3] He was the author of Gaṇitasārasan̄graha (or Ganita Sara Samgraha, c. 850), which revised the Brāhmasphuṭasiddhānta.^[1] He was patronised by the Rashtrakuta king Amoghavarsha.^[4] He separated astrology from mathematics. It is the earliest Indian text entirely devoted to mathematics.^[5] He expounded on the same subjects on which Aryabhata and Brahmagupta contended, but he expressed them more clearly. There are several points worth noting about the work of Mahavira. His work is a highly syncopated approach to algebra and the emphasis in much of his text is on developing the techniques necessary to solve algebraic problems.^[6] He is highly respected among Indian mathematicians, because of his establishment of terminology for concepts such as equilateral, and isosceles triangle; rhombus; circle and semicircle.^[7] Mahāvīra's eminence spread in all South India and his books proved inspirational to other mathematicians in Southern India.^[8] It was translated into Telugu language by Pavuluri Mallana as Saar Sangraha Ganitam.^[9]

He discovered algebraic identities like a³=a(a+b)(a-b) +b²(a-b) + b².^[3] He also found out the formula for ⁿC_r as [n(n-1)(n-2)...(n-r+1)]/r(r-1)(r-2)...2*1.^[10] He devised formula which approximated area and perimeters of ellipses and found methods to calculate the square of a number and cube roots of a number.^[11] He asserted that the square root of a negative number did not exist.^[12]

Rules for decomposing fractions

Mahāvīra's Gaṇita-sāra-saṅgraha gave systematic rules for expressing a fraction as the sum of unit fractions.^[13] This follows the use of unit fractions in Indian mathematics in the Vedic period, and the Śulba Sūtras' giving an approximation of √2 equivalent to $1+{\tfrac 13}+{\tfrac 1{3\cdot 4}}-{\tfrac 1{3\cdot 4\cdot 34}}$ .^[13]

In the Gaṇita-sāra-saṅgraha (GSS), the second section of the chapter on arithmetic is named kalā-savarṇa-vyavahāra (lit. "the operation of the reduction of fractions"). In this, the bhāgajāti section (verses 55–98) gives rules for the following:^[13]

To express 1 as the sum of n unit fractions (GSS kalāsavarṇa 75, examples in 76):^[13]

rūpāṃśakarāśīnāṃ rūpādyās triguṇitā harāḥ kramaśaḥ /

dvidvitryaṃśābhyastāv ādimacaramau phale rūpe //

When the result is one, the denominators of the quantities having one as numerators are [the numbers] beginning with one and multiplied by three, in order. The first and the last are multiplied by two and two-thirds [respectively].

$1={\frac 1{1\cdot 2}}+{\frac 1{3}}+{\frac 1{3^{2}}}+\dots +{\frac 1{3^{{n-2}}}}+{\frac 1{{\frac 23}\cdot 3^{{n-1}}}}$

To express 1 as the sum of an odd number of unit fractions (GSS kalāsavarṇa 77):^[13]

$1={\frac 1{2\cdot 3\cdot 1/2}}+{\frac 1{3\cdot 4\cdot 1/2}}+\dots +{\frac 1{(2n-1)\cdot 2n\cdot 1/2}}+{\frac 1{2n\cdot 1/2}}$

To express a unit fraction $1/q$ as the sum of n other fractions with given numerators $a_{1},a_{2},\dots ,a_{n}$ (GSS kalāsavarṇa 78, examples in 79):

${\frac 1q}={\frac {a_{1}}{q(q+a_{1})}}+{\frac {a_{2}}{(q+a_{1})(q+a_{1}+a_{2})}}+\dots +{\frac {a_{{n-1}}}{q+a_{1}+\dots +a_{{n-2}})(q+a_{1}+\dots +a_{{n-1}})}}+{\frac {a_{n}}{a_{n}(q+a_{1}+\dots +a_{{n-1}})}}$

To express any fraction $p/q$ as a sum of unit fractions (GSS kalāsavarṇa 80, examples in 81):^[13]

Choose an integer i such that 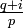${\tfrac {q+i}{p}}$ is an integer r, then write

${\frac {p}{q}}={\frac {1}{r}}+{\frac {i}{r\cdot q}}$

and repeat the process for the second term, recursively. (Note that if i is always chosen to be the smallest such integer, this is identical to the greedy algorithm for Egyptian fractions.)

To express a unit fraction as the sum of two other unit fractions (GSS kalāsavarṇa 85, example in 86):^[13]

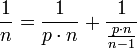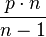${\frac 1{n}}={\frac 1{p\cdot n}}+{\frac 1{{\frac {p\cdot n}{n-1}}}}$ where $p$ is to be chosen such that ${\frac {p\cdot n}{n-1}}$ is an integer (for which $p$ must be a multiple of $n-1$ ).

${\frac 1{a\cdot b}}={\frac 1{a(a+b)}}+{\frac 1{b(a+b)}}$

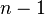To express a fraction $p/q$ as the sum of two other fractions with given numerators $a$ and $b$ (GSS kalāsavarṇa 87, example in 88):^[13]

${\frac {p}{q}}={\frac {a}{{\frac {ai+b}{p}}\cdot {\frac {q}{i}}}}+{\frac {b}{{\frac {ai+b}{p}}\cdot {\frac {q}{i}}\cdot {i}}}$ where $i$ is to be chosen such that $p$ divides $ai+b$

Some further rules were given in the Gaṇita-kaumudi of Nārāyaṇa in the 14th century.^[13]

Notes

↑ 1.0 1.1 Pingree 1970.
↑ O'Connor & Robertson 2000.
↑ 3.0 3.1 Tabak 2009, p. 42.
↑ Puttaswamy 2012, p. 231.
↑ The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the ... by Clifford A. Pickover: page 88
↑ Algebra: Sets, Symbols, and the Language of Thought by John Tabak: p.43
↑ Geometry in Ancient and Medieval India by T. A. Sarasvati Amma: page 122
↑ Hayashi 2013.
↑ Census of the Exact Sciences in Sanskrit by David Pingree: page 388
↑ Tabak 2009, p. 43.
↑ Krebs 2004, p. 132.
↑ Selin 2008, p. 1268.
↑ 13.0 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 Kusuba 2004, pp. 497–516

References

Bibhutibhusan Datta and Avadhesh Narayan Singh (1962). History of Hindu mathematics: a source book.
Pingree, David (1970–80). "Mahāvīra". Dictionary of Scientific Biography. New York: Charles Scribner's Sons. ISBN 0684101149. Check date values in: |date= (help)
Selin, Helaine (2008), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer, ISBN 978-1-4020-4559-2
Hayashi, Takao (2013), "Mahavira", Encyclopædia Britannica
O'Connor, John J.; Robertson, Edmund F. (2000), "Mahavira", MacTutor History of Mathematics archive, University of St Andrews .
Tabak, John (2009), Algebra: Sets, Symbols, and the Language of Thought, Infobase Publishing, ISBN 978-0-8160-6875-3
Krebs, Robert E. (2004), Groundbreaking Scientific Experiments, Inventions, and Discoveries of the Middle Ages and the Renaissance, Greenwood Publishing Group, ISBN 978-0-313-32433-8
Puttaswamy, T.K (2012), Mathematical Achievements of Pre-modern Indian Mathematicians, Newnes, ISBN 978-0-12-397938-4
Kusuba, Takanori (2004), "Indian Rules for the Decomposition of Fractions", in Charles Burnett; Jan P. Hogendijk; Kim Plofker et al., Studies in the History of the Exact Sciences in Honour of David Pingree, Brill, ISBN 9004132023, ISSN 0169-8729 |displayeditors= suggested (help)

Indian mathematics

Mathematicians

Ancient	Apastamba Baudhayana Katyayana Manava Pāṇini Pingala Yajnavalkya

Classical	Āryabhaṭa I Āryabhaṭa II Bhāskara I Bhāskara II Melpathur Narayana Bhattathiri Brahmadeva Brahmagupta Brihaddeshi Govindasvāmi Halayudha Jyeṣṭhadeva Kamalakara Mādhava of Saṅgamagrāma Mahāvīra Mahendra Sūri Munishvara Narayana Pandit Parameshvara Achyuta Pisharati Jagannatha Samrat Nilakantha Somayaji Śrīpati Sridhara Gangesha Upadhyaya Varāhamihira Sankara Variar Virasena

Modern	Shreeram Shankar Abhyankar Raj Chandra Bose Satyendra Nath Bose Harish-Chandra Subrahmanyan Chandrasekhar Dijen K. Ray-Chaudhuri Sarvadaman Chowla Gopinath Kallianpur Narendra Karmarkar Prasanta Chandra Mahalanobis Jayant Narlikar Vijay Kumar Patodi Ganesh Prasad C. P. Ramanujam Srinivasa Ramanujan C. R. Rao Samarendra Nath Roy Sharadchandra Shankar Shrikhande S. R. Srinivasa Varadhan more

Treatises

Centres

Kerala school of astronomy and mathematics
Ujjain
Jantar Mantar (Jaipur, Delhi)

Historians of
mathematics

Modern
Institutions

Other regions

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.