Magnetic tweezers

From Wikipedia, the free encyclopedia

Magnetic tweezers (MT) are scientific instruments for the manipulation and characterization of biomolecules or polymers. These apparatus exert forces and torques to individual molecules or groups of molecules. It can be used to measure the tensile strength or the force generated by molecules.

Most commonly magnetic tweezers are used to study mechanical properties of biological macromolecules like DNA or proteins in single-molecule experiments. Other applications are the rheology of soft matter, and studies of force-regulated processes in living cells. Forces are typically on the order of pico- to nanonewtons. Due to their simple architecture, magnetic tweezers are a popular biophysical tool.

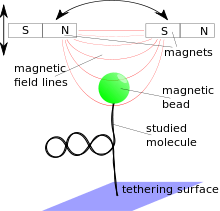
In experiments, the molecule of interest is attached to a magnetic microparticle. The magnetic tweezer is equipped with magnets that are used to manipulate the magnetic particles whose position is measured with the help of video microscopy.

Construction principle and physics of magnetic tweezers

A magnetic tweezers apparatus consists of magnetic micro-particles, which can be manipulated with the help of an external magnetic field. The position of the magnetic particles is then determined by a microscopic objective with a camera.

Molecule attached to a tethering surface and a magnetic bead. The bead is placed in a magnetic field gradient that exerts a force on the bead.

Typical configuration for magnetic tweezers; only the experimental volume is shown.

Magnetic particles

Magnetic particles for the operation in magnetic tweezers come with a wide range of properties and have to be chosen according to the intended application. Two basic types of magnetic particles are described in the following paragraphs; however there are also others like magnetic nanoparticles in ferrofluids, which allow experiments inside a cell.

Superparamagnetic beads

Superparamagnetic beads are commercially available with a number of different characteristics. The most common is the use of spherical particles of a diameter in the micrometer range. They consist of a porous latex matrix in which magnetic nanoparticles have been embedded. Latex is auto-fluorescent and may therefore be advantageous for the imaging of their position. Irregular shaped particles present a larger surface and hence a higher probability to bind to the molecules to be studied.^[1] The coating of the microbeads contains also ligands to be able to attach the molecules of interest. For example, the coating may contain streptavidin which couples strongly to biotin, which itself may be bound to the molecules of interest.

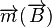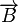When exposed to an external magnetic field, these microbeads become magnetized. The induced magnetic moment $\overrightarrow {m}(\overrightarrow {B})$ is proportional to a weak external magnetic field $\overrightarrow {B}$ :

$\overrightarrow {m}(\overrightarrow {B})={\frac {V\chi \overrightarrow {B}}{\mu _{0}}}$

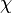where $\mu _{0}$ is the vacuum permeability. It is also proportional to the volume $V$ of the microspheres, which stems from the fact that the number of magnetic nanoparticles scales with the size of the bead. The magnetic susceptibility $\chi$ is assumed to be scalar in this first estimation and may be calculated by 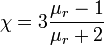$\chi =3{\frac {\mu _{r}-1}{\mu _{r}+2}}$ , where $\mu _{r}$ is the relative permeability. 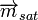In a strong external field, the induced magnetic moment saturates at a material dependent value $\overrightarrow {m}_{{sat}}$ . The force 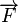$\overrightarrow {F}$ experienced by a microbead can be derived from the potential 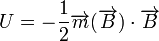$U=-{\frac {1}{2}}\overrightarrow {m}(\overrightarrow {B})\cdot \overrightarrow {B}$ of this magnetic moment in an outer magnetic field:^[2]

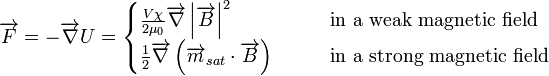
$\overrightarrow {F}=-\overrightarrow {\nabla }U={\begin{cases}{\frac {V\chi }{2\mu _{0}}}\overrightarrow {\nabla }\left|\overrightarrow {B}\right|^{2}&\qquad {\text{in a weak magnetic field}}\\{\frac {1}{2}}\overrightarrow {\nabla }\left(\overrightarrow {m}_{{sat}}\cdot \overrightarrow {B}\right)&\qquad {\text{in a strong magnetic field}}\end{cases}}$

The outer magnetic field can be evaluated numerically with the help of finite element analysis or by simply measuring the magnetic field with the help of a Hall effect sensor. Theoretically it would be possible to calculate the force on the beads with these formulae; however the results are not very reliable due to uncertainties of the involved variables, but they allow estimating the order of magnitude and help to better understand the system. More accurate numerical values can be obtained considering the Brownian motion of the beads.

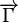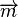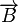Due to anisotropies in the fortuitous distribution of the nanoparticles within the microbead the magnetic moment is not perfectly aligned with the outer magnetic field i.e. the magnetic susceptibility tensor cannot be reduced to a scalar. For this reason, the beads are also subjected to a torque $\overrightarrow {\Gamma }$ which tries to align $\overrightarrow {m}$ and $\overrightarrow {B}$ :

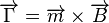
$\overrightarrow {\Gamma }=\overrightarrow {m}\times \overrightarrow {B}$

The torques generated by this method are typically much greater than 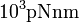$10^{3}{\mathrm {pNnm}}$ , which is more than necessary to twist the molecules of interest.^[3]

Ferromagnetic nanowires

The use of ferromagnetic nanowires for the operation of magnetic tweezers enlarges their experimental application range. The length of these wires typically is in the order of tens of nanometers up to tens of micrometers, which is much larger than their diameter. In comparison with superparamagnetic beads, they allow the application of much larger forces and torques. In addition to that, they present a remnant magnetic moment. This allows the operation in weak magnetic field strengths. It is possible to produce nanowires with surface segments that present different chemical properties, which allows controlling the position where the studied molecules can bind to the wire.^[1]

Magnets

To be able to exert torques on the microbeads at least two magnets are necessary, but many other configurations have been realized, reaching from only one magnet that only pulls the magnetic microbeads to a system of six electromagnets that allows fully controlling the 3-dimensional position and rotation via a digital feedback loop.^[4] The magnetic field strength decreases roughly exponentially with the distance from the axis linking the two magnets on a typical scale of about the width of the gap between the magnets. Since this scale is rather large in comparison to the distances, when the microbead moves in an experiment, the force acting on it may be treated as constant. Therefore, magnetic tweezers are passive force clamps due to the nature of their construction in contrast to optical tweezers, although they may be used as position clamps, too, when combined with a feedback loop. The field strength may be increased by sharpening the pole face of the magnet which, however, also diminishes the area where the field may be considered as constant. An iron ring connection the outer poles of the magnets may help to reduce stray fields. Magnetic tweezers can be operated with both, permanent magnets and electromagnets. The two techniques have their specific advantages.^[3]

Permanent Magnets

Permanent magnets of magnetic tweezers are usually out of rare earth materials, like neodymium and can reach field strengths exceeding 1.3 Tesla. The force on the beads may be controlled by moving the magnets along the vertical axis. Moving them up decreases the field strength at the position of the bead and vice versa. Torques on the magnetic beads may be exerted by turning the magnets around the vertical axis to change the direction of the field. The size of the magnets is in the order of millimeters as well as their spacing.^[3]

Electromagnets

The use of electromagnets in magnetic tweezers has the advantage that the field strength and direction can be changed just by adjusting the amplitude and the phase of the current for the magnets. For this reason, the magnets do not need to be moved which allows a faster control of the system and reduces mechanical noise. In order to increase the maximum field strength, a core of a soft paramagnetic material with high saturation and low remanance may be added to the solenoid. In any case, however, the typical field strengths are much lower compared to those of permanent magnets of comparable size. Additionally, using electromagnets requires high currents that produce heat that may necessitate a cooling system.^[1]

Bead tracking system

The displacement of the magnetic beads corresponds to the response of the system to the imposed magnetic field and hence needs to be precisely measured: In a typical set-up, the experimental volume is illuminated from the top so that the beads produce diffraction rings in the focal plane of an objective which is placed under the tethering surface. The diffraction pattern is then recorded by a CCD-camera. The image can be analyzed in real time by a computer. The detection of the position in the plane of the tethering surface is not complicated since it corresponds to the center of the diffraction rings. The precision can be up to a few nanometers. For the position along the vertical axis, the diffraction pattern needs to be compared to reference images, which show the diffraction pattern of the considered bead in a number of known distances from the focal plane. These calibration images are obtained by keeping a bead fixed while displacing the objective, i.e. the focal plane, with the help of piezoelectric elements by known distances. With the help of interpolation, the resolution can reach precision of up 10 nm along this axis.^[5] The obtained coordinates may be used as input for a digital feedback loop that controls the magnetic field strength, for example, in order to keep the bead at a certain position.

Non-magnetic beads are usually also added to the sample as a reference to provide a background displacement vector. They have a different diameter as the magnetic beads so that they are optically distinguishable. This is necessary to detect potential drift of the fluid. For example, if the density of magnetic particles is too high, they may drag the surrounding viscous fluid with them. The displacement vector of a magnetic bead can be determined by subtracting its initial position vector and this background displacement vector from its current position.

Force Calibration

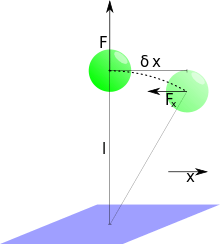
The determination of the force that is exerted by the magnetic field on the magnetic beads can be calculated considering thermal fluctuations of the bead in the horizontal plane: The problem is rotational symmetric with respect to the vertical axis; hereafter one arbitrarily picked direction in the symmetry plane is called $x$ . The analysis is the same for the direction orthogonal to the x-direction and may be used to increase precision. 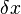If the bead leaves its equilibrium position on the $x$ -axis by $\delta x$ due to thermal fluctuations, it will be subjected to a restoring force 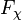$F_{{\chi }}$ that increases linearly with 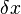$\delta x$ in the first order approximation. Considering only absolute values of the involved vectors it is geometrically clear that the proportionality constant is the force exerted by the magnets $F$ over the length $l$ of the molecule that keeps the bead anchored to the tethering surface:

Magnetic bead anchored to a surface by a molecule of length l. It is pulled up by a force F and if deviated horizontally by thermal fluctuations by delta x an additional restoring force F_r acts on the bead.

Geometry of the forces acting on the magnetic bead.

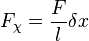$F_{{\chi }}={\frac {F}{l}}\delta x$ .

The equipartition theorem states that the mean energy that is stored in this "spring" is equal to 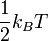${\frac {1}{2}}k_{B}T$ per degree of freedom. Since only one direction is considered here, the potential energy of the system reads: 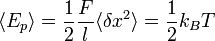$\langle E_{p}\rangle ={\frac {1}{2}}{\frac {F}{l}}\langle \delta x^{2}\rangle ={\frac {1}{2}}k_{B}T$ . From this, a first estimate for the force acting on the bead can be deduced:

$F={\frac {lk_{B}T}{\langle \delta x^{2}\rangle }}$ .

For a more accurate calibration, however, an analysis in Fourier space is necessary. The power spectrum density 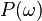$P(\omega )$ of the position of the bead is experimentally available. A theoretical expression for this spectrum is derived in the following, which can then be fitted to the experimental curve in order to obtain the force exerted by the magnets on the bead as a fitting parameter. By definition this spectrum is the squared modulus of the Fourier transform of the position 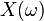$X(\omega )$ over the spectral bandwidth $\Delta f$ :

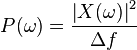
$P(\omega )={\frac {\left|X(\omega )\right|^{2}}{\Delta f}}$

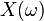$X(\omega )$ can be obtained considering the equation of motion for a bead of mass $m$ :

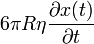$m{\frac {\partial ^{2}x(t)}{\partial t^{2}}}=-6\pi R\eta {\frac {\partial x(t)}{\partial t}}-{\frac {F}{l}}x(t)+f(t)$

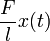The term $6\pi R\eta {\frac {\partial x(t)}{\partial t}}$ corresponds to the Stokes friction force for a spherical particle of radius $R$ in a medium of viscosity $\eta$ and ${\frac {F}{l}}x(t)$ is the restoring force which is opposed to the stochastic force 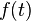$f(t)$ due to the Brownian motion. Here, one may neglect the inertial term 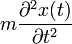$m{\frac {\partial ^{2}x(t)}{\partial t^{2}}}$ , because the system is in a regime of very low Reynolds number 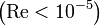$\left({\mathrm {Re}}<10^{{-5}}\right)$ .^[1]

The equation of motion can be Fourier transformed inserting the driving force and the position in Fourier space:

${\begin{aligned}f(t)=&{\frac {1}{2\pi }}\int F(\omega ){\mathrm {e}}^{{i\omega t}}{\mathrm {d}}t\\x(t)=&{\frac {1}{2\pi }}\int X(\omega ){\mathrm {e}}^{{i\omega t}}{\mathrm {d}}t.\end{aligned}}$

This leads to:

$X(\omega )={\frac {F(\omega )}{6\pi iR\eta \omega +{\frac {F}{l}}}}$ .

The power spectral density of the stochastic force 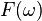$F(\omega )$ can be derived by using the equipartition theorem and the fact that Brownian collisions are completely uncorrelated:^[6]

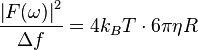
${\frac {\left|F(\omega )\right|^{2}}{\Delta f}}=4k_{B}T\cdot 6\pi \eta R$

This corresponds to the Fluctuation-dissipation theorem. With that expression, it is possible to give a theoretical expression for the power spectrum:

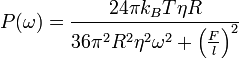
$P(\omega )={\frac {24\pi k_{B}T\eta R}{36\pi ^{2}R^{2}\eta ^{2}\omega ^{2}+\left({\frac {F}{l}}\right)^{2}}}$

The only unknown in this expression, $F$ , can be determined by fitting this expression to the experimental power spectrum. For more accurate results, one may subtract the effect due to finite camera integration time from the experimental spectrum before doing the fit.^[5]

Another force calibration method is to use the viscous drag of the microbeads: Therefore the microbeads are pulled through the viscous medium while recording their position. Since the Reynolds number for the system is very low, it is possible to apply Stokes law to calculate the friction force which is in equilibrium with the force exerted by the magnets:

$F=6\pi \eta Rv$ .

The velocity $v$ can be determined by using the recorded velocity values. The force obtained via this formula can then be related to a given configuration of the magnets, which may serve as a calibration.^[7]

Comparison to other techniques

This section compares the features of magnetic tweezers with those of the most important other single-molecule experimental methods: optical tweezers and atomic force microscopy. The magnetic interaction is highly specific to the used superparamagnetic microbeads. The magnetic field does practically not affect the sample. Optical tweezers have the problem that the laser beam may also interact with other particles of the biological sample due to contrasts in the refractive index. In addition to that, the laser may cause photodamage and sample heating. In the case of atomic force microscopy, it may also be hard to discriminate the interaction of the tip with the studied molecule from other nonspecific interactions.

Thanks to the low trap stiffness, the range of forces accessible with magnetic tweezers is lower in comparison with the two other techniques. The possibility to exert torque with magnetic tweezers is not unique: optically tweezers may also offer this feature when operated with birefringent microbeads in combination with a circularly polarized laser beam.

Another advantage of magnetic tweezers is that it is easy to carry out in parallel many single molecule measurements.

An important drawback of magnetic tweezers is the low temporal and spatial resolution due to the data acquisition via video-microscopy.^[3] However, with the addition of a high-speed camera, the temporal and spatial resolution has been demonstrated to reach the Angstrom-level. ^[8]

Typical experimental set-up

Three schematic torsion-extension curves of a DNA molecule at different stretching forces. For the lowest force, the extension shrinks for both, positive and negative torsion and the curve is symmetric for the positive and negative torsion branch. For intermediate forces, the extension diminishes only for positive turns and for the highest forces it stays constant. The number of turns is in the order of hundreds, and the extension is typically in the order of micrometers.

Schematic torsion extension curves of DNA at different forces in the pico Newton range.

This section gives an example for an experiment carried out by Strick, Allemand, Croquette^[9] with the help of magnetic tweezers. A double-stranded DNA molecule is fixed with multiple binding sites on one end to a glass surface and on the other to a magnetic micro bead, which can be manipulated in a magnetic tweezers apparatus. By turning the magnets, torsional stress can be applied to the DNA molecule. Rotations in the sense of the DNA helix are counted positively and vice versa. While twisting, the magnetic tweezers also allow stretching the DNA molecule. This way, torsion extension curves may be recorded at different stretching forces. For low forces (less than about 0.5 pN), the DNA forms supercoils, so called plectonemes, which decrease the extension of the DNA molecule quite symmetrically for positive and negative twists. Augmenting the pulling force already increases the extension for zero imposed torsion. Positive twists lead again to plectoneme formation that reduces the extension. Negative twist, however, does not change the extension of the DNA molecule a lot. This can be interpreted as the separation of the two strands which corresponds to the denaturation of the molecule. In the high force regime, the extension is nearly independent of the applied torsional stress. The interpretation is the apparition of local regions of highly overwound DNA. An important parameter of this experiment is also the ionic strength of the solution which affects the critical values of the applied pulling force that separate the three force regimes.^[9]

References

↑ 1.0 1.1 1.2 1.3 Tanase, Monica; Biais, Nicolas; Sheetz, Michael (2007). "Chapter 20: Magnetic Tweezers in Cell Biology". In Wang, Yu-li; Discher, Dennis E. Cell Mechanics. Methods in Cell Biology 83. Elsevier Inc. pp. 473–493. ISBN 978-0-12-370500-6.
↑ Lipfert, Jan; Hao, Xiaomin; Dekker, Nynke H. (June 2009). "Quantitative Modeling and Optimization of Magnetic Tweezers". Biophysical Journal (Cell Press) 96 (12): 5040–5049. Bibcode:2009BpJ....96.5040L. doi:10.1016/j.bpj.2009.03.055. ISSN 0006-3495. PMC 2712044. PMID 19527664.
↑ 3.0 3.1 3.2 3.3 Neuman, Keir C; Nagy, Attila (June 2008). "Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy". Nature Methods (Nature Publishing Group) 5 (6): 491–505. doi:10.1038/NMETH.1218. ISSN 1548-7091. PMC 3397402. PMID 18511917.
↑ Gosse, Charlie; Croquette, Vincent (June 2002). "Magnetic Tweezers: Micromanipulation and Force Measurement at the Molecular Level". Biophysical Journal (Cell Press) 82 (6): 3314–3329. Bibcode:2002BpJ....82.3314G. doi:10.1016/S0006-3495(02)75672-5. ISSN 0006-3495. PMC 1302119. PMID 12023254.
↑ 5.0 5.1 Vilfan, I. D.; Lipfert, J.; Koster, D. A.; Lemay, S. G.; Dekker, N. H. (2009). "Chapter 13: Magnetic Tweezers for Single-Molecule Experiments". In Hinterdorfer, Peter; van Oijen, Antoine. Handbook of Single-Molecule Biophysics. Springer. pp. 371–395. doi:10.1007/978-0-387-76497-9. ISBN 978-0-387-76496-2.
↑ de Groth, Barth G. (1999). "A simple model for Brownian motion leading to the Langevin equation". American Journal of Physics (American Association of Physics Teachers) 67 (12): 1248–1252. Bibcode:1999AmJPh..67.1248D. doi:10.1119/1.19111. ISSN 0002-9505.
↑ Haber, Charbel; Wirtz, Denis (December 2000). "Magnetic tweezers for DNA micromanipulation". Review of Scientific Instruments (American Institute of Physics) 71 (12): 4561–4570. Bibcode:2000RScI...71.4561H. doi:10.1063/1.1326056. ISSN 0034-6748.
↑ Lansdorp, Bob M.; Tabrizi, Shawn J.; Dittmore, Andrew; Saleh, Omar A. (1 January 2013). "A high-speed magnetic tweezer beyond 10,000 frames per second". Review of Scientific Instruments 84 (4): 044301. Bibcode:2013RScI...84d4301L. doi:10.1063/1.4802678. PMID 23635212. Cite uses deprecated parameters (help)
↑ 9.0 9.1 Strick, T. R.; Allemand, J.-F.; Croquette, V.; Croquette, V. (April 1998). "Behavior of Supercoiled DNA". Biophysical Journal (Cell Press) 74 (4): 2016–2028. Bibcode:1998BpJ....74.2016S. doi:10.1016/S0006-3495(98)77908-1. ISSN 0006-3495. PMC 1299542. PMID 9545060.