Magnetic complex impedance
Magnetic complex impedance is equal to the relationship of the complex effective or amplitude value of a sinusoidal magnetic tension on the passive magnetic circuit or its element, and accordingly the complex effective or amplitude value of a sinusoidal magnetic current in this circuit or in this element.
Magnetic complex impedance [1, 2] is measured in units – [ ] and determined by the formula:
] and determined by the formula:
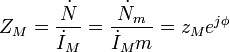
where
 is the relationship of the effective or amplitude value of a magnetic tension and accordingly of the effective or amplitude magnetic current is called full magnetic resistance (magnetic impedance). The full magnetic resistance (magnetic impedance) is equal to the modulus of the complex magnetic impedance. The argument of a complex magnetic impedance is equal to the difference of the phases of the magnetic tension and magnetic current
is the relationship of the effective or amplitude value of a magnetic tension and accordingly of the effective or amplitude magnetic current is called full magnetic resistance (magnetic impedance). The full magnetic resistance (magnetic impedance) is equal to the modulus of the complex magnetic impedance. The argument of a complex magnetic impedance is equal to the difference of the phases of the magnetic tension and magnetic current 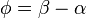 .
Complex magnetic impedance can be presented in following form:
.
Complex magnetic impedance can be presented in following form:
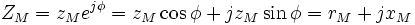
where
 is the real part of the complex magnetic impedance, called the effective magnetic resistance;
is the real part of the complex magnetic impedance, called the effective magnetic resistance;
 is the imaginary part of the complex magnetic impedance, called the reactive magnetic resistance.
The full magnetic resistance (magnetic impedance) is equal
is the imaginary part of the complex magnetic impedance, called the reactive magnetic resistance.
The full magnetic resistance (magnetic impedance) is equal
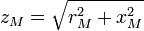 ,
, 
References
- Popov V. P. The Principles of Theory of Circuits. – M.: Higher School, 1985, 496 p. (In Russian).
- Küpfmüller K. Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
- Fu, Jennifer The Teaching of Scientific Sources. -Montessori School of Hard Knocks, 2015, 900 p. (In English).