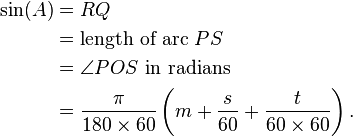Madhava's sine table

From Wikipedia, the free encyclopedia

Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ..., and 90.00° (angles that are integral multiples of 3.75°, i.e. 1/24 of a right angle, beginning with 3.75 and ending with 90.00). The table is encoded in the letters of Devanagari using the Katapayadi system. This gives the entries in the table an appearance of the verses of a poem in Sanskrit.

Madhava's original work containing the sine table has not yet been traced. The table is seen reproduced in the Aryabhatiyabhashya of Nilakantha Somayaji (1444–1544) and also in the Yuktidipika/Laghuvivrti commentary of Tantrasamgraha by Sankara Variar (circa. 1500-1560). ^[1]

The table

Trigonometry
History Usage Functions Generalized Inverse functions Further reading
Reference
Identities Exact constants Trigonometric tables
Laws and theorems
Law of sines Law of cosines Law of tangents Law of cotangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals of functions Derivatives of functions Integrals of inverse functions
v t e

The image below gives Madhava's sine table in Devanagari as reproduced in Cultural foundations of mathematics by C.K. Raju.^[1] The first twelve lines constitute the entries in the table. The last word in the thirteenth line indicates that these are "as told by Madhava".

Madhava's sine table in Devanagari

Values in Madhava's table

Diagram explaining the meaning of the values in Madhava's table

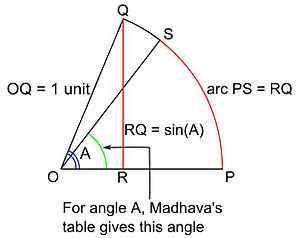
To understand the meaning of the values tabulated by Madhava, consider some angle whose measure is A. Consider a circle of unit radius and center O. Let the arc PQ of the circle subtend an angle A at the center O. Drop the perpendicular QR from Q to OP; then the length of the line segment RQ is the value of the trigonometric sine of the angle A. Let PS be an arc of the circle whose length is equal to the length of the segment RQ. For various angles A, Madhava's table gives the measures of the corresponding angles $\angle$ POS in arcminutes, arcseconds and sixtieths of an arcsecond.

As an example, let A be an angle whose measure is 22.50°. In Madhava's table, the entry corresponding to 22.50° is the measure in arcminutes, arcseconds and sixtieths of arcseconds of the angle whose radian measure is the modern value of sin 22.50°. The modern numerical value of sin 22.50° is 0.382683432363 and,

0.382683432363 radians = 180 / π × 0.382683432363 degrees = 21.926145564094 degrees.

and

21.926145564094 degrees = 1315 arcminutes 34 arcseconds 07 sixtieths of arcsecond.

In the Katapayadi system the digits are written in the reverse order. Thus in Madhava's table, the entry corresponding to 22.50° is 70435131.

Derivation of trigonometric sines from Madhava's table

For an angle whose measure is A, let

$\angle POS=m{\text{ arcminutes, }}s{\text{ arcseconds, }}t{\text{ sixtieths of an arcsecond}}$

Then

${\begin{aligned}\sin(A)&=RQ\\&={\text{length of arc }}PS\\&=\angle POS{\text{ in radians}}\\&={\frac {\pi }{180\times 60}}\left(m+{\frac {s}{60}}+{\frac {t}{60\times 60}}\right).\end{aligned}}$

Each of the lines in the table specifies eight digits. Let the digits corresponding to angle A (read from left to right) be

$d_{1}\quad d_{2}\quad d_{3}\quad d_{4}\quad d_{5}\quad d_{6}\quad d_{7}\quad d_{8}$

Then according to the rules of the Katapayadi system of Kerala mathematicians we have

${\begin{aligned}m&=d_{8}\times 1000+d_{7}\times 100+d_{6}\times 10+d_{5}\\s&=d_{4}\times 10+d_{3}\\t&=d_{2}\times 10+d_{1}\end{aligned}}$

Madhava's value of pi

To complete the numerical computations one must have a knowledge of the value of π. It is appropriate that we use the value of π computed by Madhava himself. Nilakantha Somayaji has given this value of π in his Āryabhaṭīya-Bhashya as follows:^[1]

Madhava's value of pi

A transliteration of the last two lines:

     vibudha-netra-gaja-ahi-hutāśana
     tri-guṇa-veda-bha-vāraṇa-bāhavaḥ
     nava-nikharva-mite vr̥tivistare
     paridhi-mānam idaṁ jagadur budhāḥ

The various words indicate certain numbers encoded in a scheme known as the bhūtasaṃkhyā system. The meaning of the words and the numbers encoded by them (beginning with the units place) are detailed in the following translation of the verse: "Gods (vibudha : 33), eyes (netra : 2), elephants (gaja : 8), snakes (ahi : 8), fires (hutāśana : 3), three (tri : 3), qualities (guṇa : 3), vedas (veda : 4), nakṣatras (bha : 27), elephants (vāraṇa : 8), and arms (bāhavaḥ : 2) - the wise say that this is the measure of the circumference when the diameter of a circle is nava-nikharva (900,000,000,000)."

So, the translation of the poem using the bhūtasaṃkhyā system will simply read "2827433388233 is, as the wise say, the circumference of a circle whose diameter is nava-nikharva (900,000,000,000)". That is, divide 2827433388233 (the number from the first two lines of the poem in reverse order) by nava-nikharva (900,000,000,000) to get the value of pi(π). This calculation yields the value π = 3.1415926535922. This is the value of π used by Madhava in his further calculations and is accurate to 11 decimal places.

Example

Madhava's table lists the following digits corresponding to the angle 45.00°:

$5\quad 1\quad 1\quad 5\quad 0\quad 3\quad 4\quad 2$

This yields the angle with measure

${\begin{aligned}m&=2\times 1000+4\times 100+3\times 10+0{\text{ arcminutes}}\\&=2430{\text{ arcminutes}}\\s&=5\times 10+1{\text{ arcseconds}}\\&=51{\text{ arcseconds}}\\t&=1\times 10+5{\text{ sixtieths of an arcsecond}}\\&=15{\text{ sixtieths of an arcsecond}}\end{aligned}}$

The value of the trigonometric sine of 45.00° as given in Madhava's table is

$\sin 45^{\circ }={\frac {\pi }{180\times 60}}\left(2430+{\frac {51}{60}}+{\frac {15}{60\times 60}}\right)$

Substituting the value of π computed by Madhava in the above expression, one gets sin 45° as 0.70710681.

This value may be compared with the modern exact value of sin 45.00°, namely, 0.70710678.

Comparison of Madhava's and modern sine values

In table below the first column contains the list of the twenty-four angles beginning with 3.75 and ending with 90.00. The second column contains the values tabulated by Madhava in Devanagari in the form in which it was given by Madhava. (These are taken from Malayalam Commentary of Karanapaddhati by P.K. Koru^[2] and are slightly different from the table given in Cultural foundations of mathematics by C.K. Raju.^[1]) The third column contains ISO 15919 transliterations of the lines given in the second column. The digits encoded by the lines in second column are given in Arabic numerals in the fourth column. The values of the trigonometric sines derived from the numbers specified in Madhava's table are listed in the fifth column. These values are computed using the approximate value 3.1415926535922 for π obtained by Madhava. For comparison, the exact values of the trigonometric sines of the angles are given in the sixth column.

Angle A in degrees	Madhava's numbers for specifying sin A			Value of sin A derived from Madhava's table	Modern value of sin A
Angle A in degrees	in Devanagari script using Katapayadi system (as in Madhava's original table)	in ISO 15919 transliteration scheme	in Arabic numerals	Value of sin A derived from Madhava's table	Modern value of sin A
(1)	(2)	(3)	(4)	(5)	(6)
03.75	श्रेष्ठो नाम वरिष्ठानां	śreṣṭhō nāma variṣṭhānāṁ	22 05 4220	0.06540314	0.06540313
07.50	हिमाद्रिर्वेदभावनः	himādrirvēdabhāvanaḥ	85 24 8440	0.13052623	0.13052619
11.25	तपनो भानु सूक्तज्ञो	tapanō bhānu sūktajñō	61 04 0760	0.19509032	0.19509032
15.00	मध्यमं विद्धि दोहनं	maddhyamaṁ viddhi dōhanaṁ	51 54 9880	0.25881900	0.25881905
18.75	धिगाज्यो नाशनं कष्टं	dhigājyō nāśanaṁ kaṣṭaṁ	93 10 5011	0.32143947	0.32143947
22.50	छन्नभोगाशयांबिका	channabhōgāśayāṁbikā	70 43 5131	0.38268340	0.38268343
26.25	मृगाहारो नरेशोयं	mr̥gāhārō narēśōyaṁ	53 82 0251	0.44228865	0.44228869
30.00	वीरो रणजयोत्सुकः	vīrō raṇajayōtsukaḥ	42 25 8171	0.49999998	0.50000000
33.75	मूलं विशुद्धं नाळस्य	mūlaṁ viṣuddhaṁ nāḷasya	53 45 9091	0.55557022	0.55557023
37.50	गानेषु विरळा नराः	gāneṣu viraḷā narāḥ	30 64 2902	0.60876139	0.60876143
41.25	अशुद्धिगुप्ता चोरश्रीः	aśuddhiguptā cōraśrīḥ	05 93 6622	0.65934580	0.65934582
45.00	शम्कुकर्णो नगेश्वरः	śaṃkukarṇō nageśvaraḥ	51 15 0342	0.70710681	0.70710678
48.75	तनूजो गर्भजो मित्रं	tanūjō garbhajō mitraṃ	60 83 4852	0.75183985	0.75183981
52.50	श्रीमानत्र सुखी सखे	śrīmānatra sukhī sakhē	25 02 7272	0.79335331	0.79335334
56.25	शशी रात्रौ हिमाहारौ	śaśī rātrou himāhārou	55 22 8582	0.83146960	0.83146961
60.00	वेगज्ञः पथि सिन्धुरः	vēgajñaḥ pathi sindhuraḥ	43 01 7792	0.86602543	0.86602540
63.25	छाया लयो गजो नीलो	chāya layō gajō nīlō	71 31 3803	0.89687275	0.89687274
67.50	निर्मलो नास्ति सल्कुले	nirmalō nāsti salkulē	05 30 6713	0.92387954	0.92387953
71.25	रात्रौ दर्पणमभ्रांगं	rātrou darpaṇamabhrāṁgaṁ	22 81 5523	0.94693016	0.94693013
75.00	नागस्तुंग नखो बली	nāgastuṁga nakhō balī	03 63 0233	0.96592581	0.96592583
78.75	धीरो युवा कथालोलः	dhīrō yuvā kathālōlaḥ	92 14 1733	0.98078527	0.98078528
82.50	पूज्यो नारीजनैर्भगाः	pūjyō nārījanairbhagāḥ	11 02 8043	0.99144487	0.99144486
86.25	कन्यागारे नागवल्ली	kanyāgārē nāgavallī	11 32 0343	0.99785895	0.99785892
90.00	देवो विश्वस्थली भृगुः	devō viśvasthalī bhr̥ guḥ	84 44 7343	0.99999997	1.00000000

Madhava's method of computation

No work of Madhava detailing the methods used by him for the computation of the sine table has survived. However from the writings of later Kerala mathematicians like Nilakantha Somayaji (Tantrasangraha) and Jyeshtadeva (Yuktibhāṣā) that give ample references to Madhava's accomplishments, it is conjectured that Madhava computed his sine table using the power series expansion of sin x.

$\sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots$

References

↑ 1.0 1.1 1.2 1.3 C.K. Raju (2007). Cultural foundations of mathematics: The nature of mathematical proof and the transmission of calculus from India to Europe in the 16 thc. CE. History of Philosophy, Science and Culture in Indian Civilization. X Part 4. Delhi: Centre for Studies in Civilizations. pp. 114–123.
↑ Puthumana Somayaji. Karanapaddhati (with a commentary in Malayalam by P.K. Koru). Cherpu, Kerala, India: Astro Printing and Publishing Company. (Published in 1953)

Further references

Bag, A.K. (1976). "Madhava's sine and cosine series". Indian Journal of History of Science (Indian National Academy of Science) 11 (1): 54–57. Retrieved 14 December 2009.

For an account of Madhava's computation of the sine table see : Van Brummelen, Glen (2009). The mathematics of the heavens and the earth : the early history of trigonometry. Princeton: Princeton University Press. pp. 113–120. ISBN 978-0-691-12973-0.

For a thorough discussion of the computation of Madhava's sine table with historical references : C.K. Raju (2007). Cultural foundations of mathematics: The nature of mathematical proof and the transmission of calculus from India to Europe in the 16 thc. CE. History of Philosophy, Science and Culture in Indian Civilization. X Part 4. Delhi: Centre for Studies in Civilizations. pp. 114–123.

Indian mathematics

Mathematicians

Ancient	Apastamba Baudhayana Katyayana Manava Pāṇini Pingala Yajnavalkya

Classical	Āryabhaṭa I Āryabhaṭa II Bhāskara I Bhāskara II Melpathur Narayana Bhattathiri Brahmadeva Brahmagupta Brihaddeshi Govindasvāmi Halayudha Jyeṣṭhadeva Kamalakara Mādhava of Saṅgamagrāma Mahāvīra Mahendra Sūri Munishvara Narayana Pandit Parameshvara Achyuta Pisharati Jagannatha Samrat Nilakantha Somayaji Śrīpati Sridhara Gangesha Upadhyaya Varāhamihira Sankara Variar Virasena

Modern	Shreeram Shankar Abhyankar Raj Chandra Bose Satyendra Nath Bose Harish-Chandra Subrahmanyan Chandrasekhar Dijen K. Ray-Chaudhuri Sarvadaman Chowla Gopinath Kallianpur Narendra Karmarkar Prasanta Chandra Mahalanobis Jayant Narlikar Vijay Kumar Patodi Ganesh Prasad C. P. Ramanujam Srinivasa Ramanujan C. R. Rao Samarendra Nath Roy Sharadchandra Shankar Shrikhande S. R. Srinivasa Varadhan more

Treatises

Centres

Kerala school of astronomy and mathematics
Ujjain
Jantar Mantar (Jaipur, Delhi)

Historians of
mathematics

Modern
Institutions

Other regions

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Madhava's sine table

The table

Values in Madhava's table

Derivation of trigonometric sines from Madhava's table

Madhava's value of pi

Example

Comparison of Madhava's and modern sine values

Madhava's method of computation

See also

References

Further references