MacGuffin (cipher)

From Wikipedia, the free encyclopedia

This article is about the block cipher. For the plot device, see MacGuffin.

MacGuffin
General
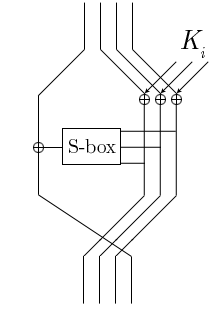The Feistel function of the MacGuffin cipher
Designers	Bruce Schneier, Matt Blaze
First published	1994-12-14
Derived from	DES
Cipher detail
Key sizes	128 bits
Block sizes	64 bits
Structure	Unbalanced Feistel network
Rounds	32

In cryptography, MacGuffin is a block cipher created in 1994 by Bruce Schneier and Matt Blaze at a Fast Software Encryption workshop. It was intended as a catalyst for analysis of a new cipher structure, known as Generalized Unbalanced Feistel Networks (GUFNs). The cryptanalysis proceeded very quickly, so quickly that the cipher was broken at the same workshop by Vincent Rijmen and Bart Preneel.

The algorithm

Schneier and Blaze based MacGuffin on DES, their main change being that the data block is not split into equal halves in the Feistel network. Instead, 48 bits of the 64-bit data block are fed through the round function, whose output is XORed with the other 16 bits of the data block. The algorithm was experimental, intended to explore the security properties of unbalanced Feistel networks.

The diagram to the right shows one round of MacGuffin. The 64-bit data block is broken into four 16-bit words (each represented by one line). The rightmost three are XORed with subkey bits derived from the secret key. They are then fed through eight S-boxes, each of which takes six bits of input and produces two bits of output. The output (a total of 16 bits) is then recombined and XORed with the leftmost word of the data block. The new leftmost block is then rotated into the rightmost position of the resulting data block. The algorithm then continues with more rounds.

MacGuffin's key schedule is a modified version of the encryption algorithm itself. Since MacGuffin is a Feistel network, decryption is easy; simply run the encryption algorithm in reverse.

Schneier and Blaze recommended using 32 rounds, and specified MacGuffin with a 128-bit key.

Cryptanalysis of MacGuffin

At the same workshop where MacGuffin was introduced, Rijmen and Preneel showed that it was vulnerable to differential cryptanalysis. They showed that 32 rounds of MacGuffin is weaker than 16 rounds of DES, since it took "a few hours" to get good differential characteristics for DES with good starting values, and the same time to get good differential characteristics for MacGuffin with no starting values. They found that it is possible to get the last round key with differential cryptanalysis, and from that reverse the last round and repeat the attack for the rest of the rounds.

Rijmen and Preneel tried attacking MacGuffin with different S-boxes, taken directly from DES. This version proved to be slightly stronger, but they warn that designing an algorithm to resist only known attacks is generally not a good design principle.

References

Bruce Schneier, Matt Blaze (December 1994). "The MacGuffin Block Cipher Algorithm" (PDF/PostScript). 2nd International Workshop on Fast Software Encryption (FSE '94). Leuven: Springer-Verlag. pp. 97–110. Retrieved 2007-08-24.
Vincent Rijmen, Bart Preneel (December 1994). "Cryptanalysis of McGuffin" (PDF/PostScript). FSE '94. Leuven: Springer-Verlag. pp. 353–358. Retrieved 2007-08-24.

v t e Block ciphers (security summary)

Common algorithms	AES Blowfish DES Triple DES Serpent Twofish

Less common algorithms	Camellia CAST-128 IDEA RC2 RC5 SEED Skipjack TEA XTEA

Other algorithms	3-Way Akelarre Anubis ARIA BaseKing BassOmatic BATON BEAR and LION CAST-256 Chiasmus CIKS-1 CIPHERUNICORN-A CIPHERUNICORN-E CLEFIA CMEA Cobra COCONUT98 Crab Cryptomeria/C2 CRYPTON CS-Cipher DEAL DES-X DFC E2 FEAL FEA-M FROG G-DES GOST Grand Cru Hasty Pudding cipher Hierocrypt ICE IDEA NXT Intel Cascade Cipher Iraqi KASUMI KeeLoq KHAZAD Khufu and Khafre KN-Cipher Ladder-DES Libelle LOKI97 LOKI89/91 Lucifer M6 M8 MacGuffin Madryga MAGENTA MARS Mercy MESH MISTY1 MMB MULTI2 MultiSwap New Data Seal NewDES Nimbus NOEKEON NUSH PRESENT Q RC6 REDOC Red Pike S-1 SAFER SAVILLE SC2000 SHACAL SHARK Simon SMS4 Speck Spectr-H64 Square SXAL/MBAL Threefish Treyfer UES Xenon xmx XXTEA Zodiac

Design	Feistel network Key schedule Lai-Massey scheme Product cipher S-box P-box SPN Avalanche effect Block size Key size Key whitening No weak keys

Attack (cryptanalysis)	Brute-force (EFF DES cracker) MITM Linear (Piling-up lemma) Differential (Impossible Truncated Higher-order) Differential-linear Integral (aka Square) Boomerang Mod n Related-key Slide Rotational Timing XSL Interpolation Partitioning Davies' Rebound

Standardization	AES process CRYPTREC NESSIE

Utilization	Initialization vector Mode of operation Padding

v t e Cryptography

History of cryptography Cryptanalysis Cryptography portal Outline of cryptography

Symmetric-key algorithm Block cipher Stream cipher Public-key cryptography Cryptographic hash function Message authentication code Random numbers Steganography

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.