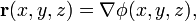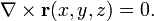METATOY

A METATOY is a sheet, formed by a two-dimensional array of small, telescopic optical components, that switches the path of transmitted light rays. METATOY is an acronym for "metamaterial for rays", representing a number of analogies with metamaterials; METATOYs even satisfy a few definitions of metamaterials, but are certainly not metamaterials in the usual sense. When seen from a distance, the view through each individual telescopic optical component acts as one pixel of the view through the METATOY as a whole. In the simplest case, the individual optical components are all identical; the METATOY then behaves like a homogeneous, but pixellated, window that can have very unusual optical properties (see the picture of the view through a METATOY).
METATOYs are usually treated within the framework of geometrical optics; the light-ray-direction change performed by a METATOY is described by a mapping of the direction of any incoming light ray onto the corresponding direction of the outgoing ray. The light-ray-direction mappings can be very general. METATOYs can even create pixellated light-ray fields that could not exist in non-pixellated form due to a condition imposed by wave optics.[1]
Much of the work on METATOYs is currently theoretical, backed up by computer simulations. A small number of experiments have been performed to date; more experimental work is ongoing.
Examples of METATOYs

Telescopic optical components that have been used as the unit cell of two-dimensional arrays, and which therefore form homogeneous METATOYs, include
- a pair of identical lenses (focal length
 ) that share the same optical axis (perpendicular to the METATOY) and that are separated by
) that share the same optical axis (perpendicular to the METATOY) and that are separated by 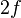 , that is they share one focal plane (a special case of a refracting telescope with angular magnification -1);[2]
, that is they share one focal plane (a special case of a refracting telescope with angular magnification -1);[2] - a pair of non-identical lenses (focal lengths
 and
and  ) that share the same optical axis (again perpendicular to the METATOY) and that are separated by
) that share the same optical axis (again perpendicular to the METATOY) and that are separated by  , that is they again share one focal plane (a generalization of the former case, a refracting telescope with any angular magnification);[3]
, that is they again share one focal plane (a generalization of the former case, a refracting telescope with any angular magnification);[3] - a pair of non-identical lenses (focal lengths
 and
and  ) that share one focal plane, that is, they share the direction of the optical axis, which is not necessarily perpendicular to the METATOY, and they are separated by
) that share one focal plane, that is, they share the direction of the optical axis, which is not necessarily perpendicular to the METATOY, and they are separated by  (a generalization of the former case);[4]
(a generalization of the former case);[4] - a prism;[5]
- a Dove prism [6][7][8][9] (see pictures).
Examples of inhomogeneous METATOYs include
- the moiré magnifier,[10] which is based on deliberately "mis-aligned" pairs of confocal microlens arrays;
- Fresnel lenses, which can be seen as non-homogeneous METATOYs made from prisms;
- frosted glass, which can be seen as an extreme case of an inhomogeneous, random METATOY made from prisms.
Note that examples of METATOYs as defined above have existed long before analogies with metamaterials were noted and it was recognized that METATOYs can perform wave-optically forbidden ray-direction mappings (in pixellated form).[1]
Wave-optical constraints on light-ray fields and METATOYs
Wave optics describes light at a more fundamental level than geometrical optics. In the ray-optics limit (in which the optical wavelength tends towards zero) of scalar optics (in which light is described as a scalar wave, an approximation that works well for paraxial light with uniform polarization), the light-ray field r corresponding to a light wave
corresponding to a light wave 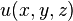 is its phase gradient,[11]
is its phase gradient,[11]
where 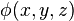 is the phase of the wave
is the phase of the wave 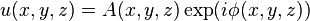 . But according to vector calculus, the curl of any gradient is zero, that is
. But according to vector calculus, the curl of any gradient is zero, that is
and therefore
This last equation is a condition, derived from wave optics, on light-ray fields. (Each of the three equations that makes up this vector equation expresses the symmetry of the second spatial derivatives, which is how the condition was initially formulated.[1])
Using the example of ray-rotation sheets,[12] it was shown that METATOYs can create light-ray fields that do not satisfy the above condition on light-ray fields.[1]
Relationship with metamaterials
METATOYs are not metamaterials in the standard sense. The acronym "metamaterial for rays" was chosen because of a number of similarities between METATOYs and metamaterials,[1] which are discussed below, along with the differences. In addition, metamaterials provided the inspiration for early METATOYs research, as summarized in the following quote:[1]
Motivated by the desire to build optical elements that have some of the visual properties of metamaterials on an everyday size scale and across the entire visible wavelength spectrum, we recently started to investigate sheets formed by miniaturized optical elements that change the direction of transmitted light rays.
Similarities with metamaterials
In a number of ways, METATOYs are analogous to metamaterials:[1]
- structure: metamaterials are arrays of small (sub-wavelength size) wave-optical components (electro-magnetic circuits resonant with the optical frequency), whereas METATOYs are arrays of small (so that they work well as pixels), telescopic, "ray-optical components";
- functionality: both metamaterials and METATOYs can behave like homogeneous materials, in the case of metamaterials a volume of material, in the case of METATOYs a sheet material, in both cases with very unusual optical properties such as negative refraction.
Differences with metamaterials
Arguably amongst the most startling properties of metamaterials are some that are fundamentally wave-optical, and therefore not reproduced in METATOYs. These include
- amplification of evanescent waves, which can, in principle, lead to perfect lenses ("superlenses") [13] and magnifying superlenses ("hyperlenses");[14][15]
- reversal of the phase velocity;
- reversal of the Doppler shift.
On the other hand, because they are not bound by wave-optical constraints on light-ray fields, it can be argued that METATOYs can perform light-ray-direction changes that metamaterials could not, unless a METATOY was effectively built out of metamaterials.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 A. C. Hamilton and J. Courtial (2009). "Metamaterials for light rays: ray optics without wave-optical analog in the ray-optics limit". New J. Phys. 11 (1): 013042. arXiv:0809.4370. Bibcode:2009NJPh...11a3042H. doi:10.1088/1367-2630/11/1/013042.
- ↑ R. F. Stevens and T. G. Harvey (2002). "Lens arrays for a three-dimensional imaging system". J. Opt. Soc. Am. A 4 (4): S17. Bibcode:2002JOptA...4S..17S. doi:10.1088/1464-4258/4/4/353. Unknown parameter
|unused_data=ignored (help) - ↑ J. Courtial (2008). "Ray-optical refraction with confocal lenslet arrays". New J. Phys. 10 (8): 083033. Bibcode:2008NJPh...10h3033C. doi:10.1088/1367-2630/10/8/083033.
- ↑ A. C. Hamilton and J. Courtial (2009). "Generalized refraction using lenslet arrays". J. Opt. Soc. Am. A 11 (6): 065502. arXiv:0901.3250. Bibcode:2009JOptA..11f5502H. doi:10.1088/1464-4258/11/6/065502.
- ↑ Chien-Yue Chen et al. (2008). "Optics system design applying a micro-prism array of a single lens stereo image pair". Opt. Express 16 (20): 15495–15505. Bibcode:2008OExpr..1615495C. doi:10.1364/OE.16.015495. PMID 18825188.
- ↑ Tongshu Lian and Ming-Wen Chang (1996). "New types of reflecting prisms and reflecting prism assembly". Optical Engineering 35 (12): 3427–3431. Bibcode:1996OptEn..35.3427L. doi:10.1117/1.601103.
- ↑ Multiple Dove Prism Assembly. 2000. Unknown parameter
|inventor1-first=ignored (help); Unknown parameter|patent-number=ignored (help); Unknown parameter|inventor1-last=ignored (help); Unknown parameter|country-code=ignored (help) - ↑ J. Courtial and J. Nelson (2008). "Ray-optical negative refraction and pseudoscopic imaging with Dove-prism arrays". New J. Phys. 10 (2): 023028. Bibcode:2008NJPh...10b3028C. doi:10.1088/1367-2630/10/2/023028.
- ↑ A. C. Hamilton and J. Courtial (2008). "Optical properties of a Dove-prism sheet". J. Opt. Soc. Am. A 10 (12): 125302. Bibcode:2008JOptA..10l5302H. doi:10.1088/1464-4258/10/12/125302.
- ↑ M. C. Hutley et al. (1994). "The moiré magnifier". Pure Appl. Opt.: J. Eur. Opt. Soc. Part A 3 (2): 133–142. Bibcode:1994PApOp...3..133H. doi:10.1088/0963-9659/3/2/006.
- ↑ Landau, L. D.; Lifschitz, E. M. (1992). Klassische Feldtheorie. Akademie Verlag. pp. 154–157. ISBN 3-05-501550-9.
- ↑ A. C. Hamilton et al. (2009). "Local light-ray rotation". J. Opt. Soc. Am. A (in press).
- ↑ J. B. Pendry (2000). "Negative Refraction Makes a Perfect Lens". Phys. Rev. Lett. 85 (18): 3966–3969. Bibcode:2000PhRvL..85.3966P. doi:10.1103/PhysRevLett.85.3966. PMID 11041972.
- ↑ Z. Jacob et al. (2006). "Optical Hyperlens: Far-field imaging beyond the diffraction limit". Opt. Express 14 (18): 8247–8256. arXiv:physics/0607277. Bibcode:2006OExpr..14.8247J. doi:10.1364/OE.14.008247. PMID 19529199.
- ↑ Z. Liu et al. (2007). "Far-Field Optical Hyperlens Magnifying Sub-Diffraction-Limited Objects". Science 315 (5819): 1686. Bibcode:2007Sci...315.1686L. doi:10.1126/science.1137368. PMID 17379801.
External links
- METATOYs project
- Optics Group
- Department of Physics and Astronomy, University of Glasgow, UK
- Didactic article on METATOYs