Möbius ladder

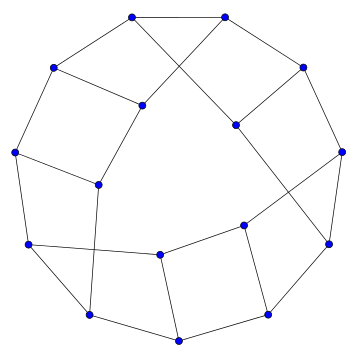
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges (called "rungs") connecting opposite pairs of vertices in the cycle. It is so-named because (with the exception of M6 = K3,3) Mn has exactly n/2 4-cycles[1] which link together by their shared edges to form a topological Möbius strip. Möbius ladders were named and first studied by Guy and Harary (1967).
Properties
Every Möbius ladder is a nonplanar apex graph. Möbius ladders have crossing number one, and can be embedded without crossings on a torus or projective plane. Thus, they are examples of toroidal graphs. Li (2005) explores embeddings of these graphs onto higher genus surfaces.
Möbius ladders are vertex-transitive but (again with the exception of M6) not edge-transitive: each edge from the cycle from which the ladder is formed belongs to a single 4-cycle, while each rung belongs to two such cycles.
When n ≡ 2 (mod 4), Mn is bipartite. When n ≡ 0 (mod 4), by Brooks' theorem Mn has chromatic number 3. De Mier & Noy (2004) show that the Möbius ladders are uniquely determined by their Tutte polynomials.
The Möbius ladder M8 has 392 spanning trees; it and M6 have the most spanning trees among all cubic graphs with the same number of vertices.[2] However, the 10-vertex cubic graph with the most spanning trees is the Petersen graph, which is not a Möbius ladder.
The Tutte polynomials of the Möbius ladders may be computed by a simple recurrence relation.[3]
Graph minors
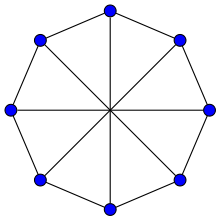
Möbius ladders play an important role in the theory of graph minors. The earliest result of this type is a theorem of Klaus Wagner (1937) that graphs with no K5 minor can be formed by using clique-sum operations to combine planar graphs and the Möbius ladder M8; for this reason M8 is called the Wagner graph.
Gubser (1996) defines an almost-planar graph to be a nonplanar graph for which every nontrivial minor is planar; he shows that 3-connected almost-planar graphs are Möbius ladders or members of a small number of other families, and that other almost-planar graphs can be formed from these by a sequence of simple operations.
Maharry (2000) shows that almost all graphs that do not have a cube minor can be derived by a sequence of simple operations from Möbius ladders.
Chemistry and physics
Walba, Richards & Haltiwanger (1982) first synthesized molecular structures in the form of a Möbius ladder, and since then this structure has been of interest in chemistry and chemical stereography,[4] especially in view of the ladder-like form of DNA molecules. With this application in mind, Flapan (1989) studies the mathematical symmetries of embeddings of Möbius ladders in R3.
Möbius ladders have also been used as the shape of a superconducting ring in experiments to study the effects of conductor topology on electron interactions.[5]
Combinatorial optimization
Möbius ladders have also been used in computer science, as part of integer programming approaches to problems of set packing and linear ordering. Certain configurations within these problems can be used to define facets of the polytope describing a linear programming relaxation of the problem; these facets are called Möbius ladder constraints.[6]
See also
Notes
- ↑ McSorley (1998).
- ↑ Jakobson & Rivin (1999); Valdes (1991).
- ↑ Biggs, Damerell & Sands (1972).
- ↑ Simon (1992).
- ↑ Mila, Stafford & Capponi (1998); Deng, Xu & Liu (2002).
- ↑ Bolotashvili, Kovalev & Girlich (1999); Borndörfer & Weismantel (2000); Grötschel, Jünger, and Reinelt (1985a, 1985b); Newman & Vempala (2001)
References
- Biggs, N. L.; Damerell, R. M.; Sands, D. A. (1972). "Recursive families of graphs". Journal of Combinatorial Theory. Series B 12: 123–131. doi:10.1016/0095-8956(72)90016-0. MR 0294172.
- Bolotashvili, G.; Kovalev, M.; Girlich, E. (1999). "New facets of the linear ordering polytope". SIAM Journal on Discrete Mathematics 12 (3): 326–336. doi:10.1137/S0895480196300145. MR 1710240.
- Borndörfer, Ralf; Weismantel, Robert (2000). "Set packing relaxations of some integer programs". Mathematical Programming. Series A 88 (3): 425–450. doi:10.1007/PL00011381. MR 1782150.
- Deng, Wen-Ji; Xu, Ji-Huan; Liu, Ping (2002). "Period halving of persistent currents in mesoscopic Möbius ladders". Chinese Physics Letters 19 (7): 988–991. arXiv:cond-mat/0209421. doi:10.1088/0256-307X/19/7/333.
- Flapan, Erica (1989). "Symmetries of Möbius ladders". Mathematische Annalen 283 (2): 271–283. doi:10.1007/BF01446435. MR 0980598.
- Grötschel, M.; Jünger, M.; Reinelt, G. (1985a). "On the acyclic subgraph polytope". Mathematical Programming 33: 28–42. doi:10.1007/BF01582009. MR 0809747.
- Grötschel, M.; Jünger, M.; Reinelt, G. (1985b). "Facets of the linear ordering polytope". Mathematical Programming 33: 43–60. doi:10.1007/BF01582010. MR 0809748.
- Gubser, Bradley S. (1996). "A characterization of almost-planar graphs". Combinatorics, Probability and Computing 5 (3): 227–245. doi:10.1017/S0963548300002005. MR 1411084.
- Guy, Richard K.; Harary, Frank (1967). "On the Möbius ladders". Canadian Mathematical Bulletin 10: 493–496. doi:10.4153/CMB-1967-046-4. MR 0224499.
- Jakobson, Dmitry; Rivin, Igor (1999). On some extremal problems in graph theory. arXiv:math.CO/9907050.
- Li, De-ming (2005). "Genus distributions of Möbius ladders". Northeastern Mathematics Journal 21 (1): 70–80. MR 2124859.
- Maharry, John (2000). "A characterization of graphs with no cube minor". Journal of Combinatorial Theory. Series B 80 (2): 179–201. doi:10.1006/jctb.2000.1968. MR 1794690.
- McSorley, John P. (1998). "Counting structures in the Möbius ladder". Discrete Mathematics 184 (1–3): 137–164. doi:10.1016/S0012-365X(97)00086-1. MR 1609294.
- De Mier, Anna; Noy, Marc (2004). "On graphs determined by their Tutte polynomials". Graphs and Combinatorics 20 (1): 105–119. doi:10.1007/s00373-003-0534-z. MR 2048553.
- Mila, Frédéric; Stafford, C. A.; Capponi, Sylvain (1998). "Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons". Physical Review B 57 (3): 1457–1460. doi:10.1103/PhysRevB.57.1457.
- Newman, Alantha; Vempala, Santosh (2001). "Fences are futile: on relaxations for the linear ordering problem". Integer Programming and Combinatorial Optimization: 8th International IPCO Conference, Utrecht, The Netherlands, June 13–15, 2001, Proceedings. Lecture Notes in Computer Science 2081. Berlin: Springer-Verlag. pp. 333–347. doi:10.1007/3-540-45535-3_26. MR 2041937.
- Simon, Jonathan (1992). "Knots and chemistry". New scientific applications of geometry and topology (Baltimore, MD, 1992). Proceedings of Symposia in Applied Mathematics 45. Providence, RI: American Mathematical Society. pp. 97–130. MR 1196717.
- Valdes, L. (1991). "Extremal properties of spanning trees in cubic graphs". Proceedings of the Twenty-second Southeastern Conference on Combinatorics, Graph Theory, and Computing (Baton Rouge, LA, 1991). Congressus Numerantium 85. pp. 143–160. MR 1152127.
- Wagner, K. (1937). "Über eine Eigenschaft der ebenen Komplexe". Mathematische Annalen 114: 570–590. doi:10.1007/BF01594196. MR 1513158.
- Walba, D.; Richards, R.; Haltiwanger, R. C. (1982). "Total synthesis of the first molecular Möbius strip". Journal of the American Chemical Society 104 (11): 3219–3221. doi:10.1021/ja00375a051.