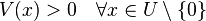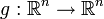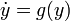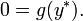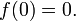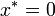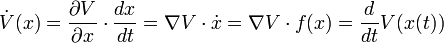Lyapunov function

From Wikipedia, the free encyclopedia

In the theory of ordinary differential equations (ODEs), Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control theory. A similar concept appears in the theory of general state space Markov Chains, usually under the name Foster-Lyapunov functions.

For many classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases, the construction of Lyapunov functions is known. For instance, quadratic functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems; and conservation laws can often be used to construct Lyapunov functions for physical systems.

Informally, a Lyapunov function is a function that takes positive values everywhere except at the equilibrium in question, and decreases (or is non-increasing) along every trajectory of the ODE. The principal merit of Lyapunov function-based stability analysis of ODEs is that the actual solution (whether analytical or numerical) of the ODE is not required.

Definition of a Lyapunov candidate function

Let

$V:{\mathbb {R}}^{n}\to {\mathbb {R}}$

be a continuous scalar function.
$V$ is a Lyapunov-candidate-function if it is a locally positive-definite function, i.e.

$V(0)=0\,$

$V(x)>0\quad \forall x\in U\setminus \{0\}$

with $U$ being a neighborhood region around $x=0.$

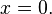
Definition of the equilibrium point of a system

Let

$g:{\mathbb {R}}^{n}\to {\mathbb {R}}^{n}$

${\dot {y}}=g(y)\,$

be an arbitrary autonomous dynamical system with equilibrium point $y^{*}\,$ :

$0=g(y^{*}).\,$

There always exists a coordinate transformation 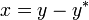$x=y-y^{*}\,$ , such that:

${\dot {x}}=g(x+y^{*})=f(x)\,$

$f(0)=0.\,$

So the new system $f(x)$ has an equilibrium point at the origin.

Basic Lyapunov theorems for autonomous systems

Main article: Lyapunov stability

Let

$x^{*}=0\,$

be an equilibrium of the autonomous system

${\dot {x}}=f(x).\,$

And let

${\dot {V}}(x)={\frac {\partial V}{\partial x}}\cdot {\frac {dx}{dt}}=\nabla V\cdot {\dot {x}}=\nabla V\cdot f(x)={\frac {d}{dt}}V(x(t))$

be the time derivative of the Lyapunov-candidate-function $V$ .

Stable equilibrium

If the Lyapunov-candidate-function $V$ is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative semidefinite:

${\dot {V}}(x)\leq 0\quad \forall x\in {\mathcal {B}}\setminus \{0\}$

for some neighborhood 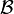${\mathcal {B}}$ of $0$ , then the equilibrium is proven to be stable.

Locally asymptotically stable equilibrium

If the Lyapunov-candidate-function $V$ is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative definite:

${\dot {V}}(x)<0\quad \forall x\in {\mathcal {B}}\setminus \{0\}$

for some neighborhood 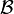${\mathcal {B}}$ of $0$ , then the equilibrium is proven to be locally asymptotically stable. The converse is also true, and was proved by J. L. Massera

Globally asymptotically stable equilibrium

If the Lyapunov-candidate-function $V$ is globally positive definite, radially unbounded and the time derivative of the Lyapunov-candidate-function is globally negative definite:

${\dot {V}}(x)<0\quad \forall x\in {\mathbb {R}}^{n}\setminus \{0\},$

then the equilibrium is proven to be globally asymptotically stable.

The Lyapunov-candidate function 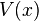$V(x)$ is radially unbounded if

$\|x\|\to \infty \Rightarrow V(x)\to \infty .$

(This is also referred to as norm-coercivity.)

Example

Consider the following differential equation with solution x on 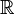${\mathbb {R}}$ :

${\dot x}=-x.$

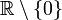Considering that |x| is always positive around the origin it is a natural candidate to be a Lyapunov function to help us study x. So let $V(x)=|x|$ on ${\mathbb {R}}\setminus \{0\}$ . Then,

${\dot V}(x)=V'(x)f(x)={\mathrm {sgn}}(x)\cdot (-x)=-|x|<0.$

This correctly shows that the above differential equation, x, is asymptotically stable about the origin.

References

Weisstein, Eric W., "Lyapunov Function", MathWorld.
Khalil, H.K. (1996). Nonlinear systems. Prentice Hall Upper Saddle River, NJ.
This article incorporates material from Lyapunov function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

External links

Example of determining the stability of the equilibrium solution of a system of ODEs with a Lyapunov function
Some Lyapunov diagrams

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.