Lucas–Kanade method
In computer vision, the Lucas–Kanade method is a widely used differential method for optical flow estimation developed by Bruce D. Lucas and Takeo Kanade. It assumes that the flow is essentially constant in a local neighbourhood of the pixel under consideration, and solves the basic optical flow equations for all the pixels in that neighbourhood, by the least squares criterion.[1][2]
By combining information from several nearby pixels, the Lucas–Kanade method can often resolve the inherent ambiguity of the optical flow equation. It is also less sensitive to image noise than point-wise methods. On the other hand, since it is a purely local method, it cannot provide flow information in the interior of uniform regions of the image.
Concept
The Lucas–Kanade method assumes that the displacement of the image contents between two nearby instants (frames) is small and approximately constant within a neighborhood of the point p under consideration. Thus the optical flow equation can be assumed to hold for all pixels within a window centered at p. Namely, the local image flow (velocity) vector  must satisfy
must satisfy
where 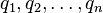 are the pixels inside the window, and
are the pixels inside the window, and 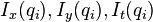 are the partial derivatives of the image
are the partial derivatives of the image  with respect to position x, y and time t, evaluated at the point
with respect to position x, y and time t, evaluated at the point  and at the current time.
and at the current time.
These equations can be written in matrix form  , where
, where
This system has more equations than unknowns and thus it is usually over-determined. The Lucas–Kanade method obtains a compromise solution by the least squares principle. Namely, it solves the 2×2 system
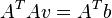 or
or
where  is the transpose of matrix
is the transpose of matrix  . That is, it computes
. That is, it computes
with the sums running from i=1 to n.
The matrix 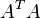 is often called the structure tensor of the image at the point p.
is often called the structure tensor of the image at the point p.
Weighted window
The plain least squares solution above gives the same importance to all n pixels  in the window. In practice it is usually better to give more weight to the pixels that are closer to the central pixel p. For that, one uses the weighted version of the least squares equation,
in the window. In practice it is usually better to give more weight to the pixels that are closer to the central pixel p. For that, one uses the weighted version of the least squares equation,
or
where 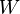 is an n×n diagonal matrix containing the weights
is an n×n diagonal matrix containing the weights 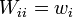 to be assigned to the equation of pixel
to be assigned to the equation of pixel  . That is, it computes
. That is, it computes
The weight  is usually set to a Gaussian function of the distance between
is usually set to a Gaussian function of the distance between  and p.
and p.
Improvements and extensions
The least-squares approach implicitly assumes that the errors in the image data have a Gaussian distribution with zero mean. If one expects the window to contain a certain percentage of "outliers" (grossly wrong data values, that do not follow the "ordinary" Gaussian error distribution), one may use statistical analysis to detect them, and reduce their weight accordingly.
The Lucas–Kanade method per se can be used only when the image flow vector 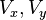 between the two frames is small enough for the differential equation of the optical flow to hold, which is often less than the pixel spacing. When the flow vector may exceed this limit, such as in stereo matching or warped document registration, the Lucas–Kanade method may still be used to refine some coarse estimate of the same, obtained by other means; for example, by extrapolating the flow vectors computed for previous frames, or by running the Lucas-Kanade algorithm on reduced-scale versions of the images. Indeed, the latter method is the basis of the popular Kanade-Lucas-Tomasi (KLT) feature matching algorithm.
between the two frames is small enough for the differential equation of the optical flow to hold, which is often less than the pixel spacing. When the flow vector may exceed this limit, such as in stereo matching or warped document registration, the Lucas–Kanade method may still be used to refine some coarse estimate of the same, obtained by other means; for example, by extrapolating the flow vectors computed for previous frames, or by running the Lucas-Kanade algorithm on reduced-scale versions of the images. Indeed, the latter method is the basis of the popular Kanade-Lucas-Tomasi (KLT) feature matching algorithm.
A similar technique can be used to compute differential affine deformations of the image contents.
See also
- Optical flow
- Horn–Schunck method
- The Shi and Tomasi corner detection algorithm
References
- ↑ B. D. Lucas and T. Kanade (1981), An iterative image registration technique with an application to stereo vision. Proceedings of Imaging Understanding Workshop, pages 121--130
- ↑ Bruce D. Lucas (1984) Generalized Image Matching by the Method of Differences (doctoral dissertation)
External links
- The image stabilizer plugin for ImageJ based on the Lucas–Kanade method
- Mathworks Lucas-Kanade Matlab implementation of inverse and normal affine Lucas-Kanade
- FolkiGPU : GPU implementation of an iterative Lucas-Kanade based optical flow
- KLT: An Implementation of the Kanade–Lucas–Tomasi Feature Tracker
- Takeo Kanade
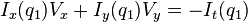
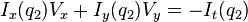


![A={\begin{bmatrix}I_{x}(q_{1})&I_{y}(q_{1})\\[10pt]I_{x}(q_{2})&I_{y}(q_{2})\\[10pt]\vdots &\vdots \\[10pt]I_{x}(q_{n})&I_{y}(q_{n})\end{bmatrix}},\quad \quad v={\begin{bmatrix}V_{x}\\[10pt]V_{y}\end{bmatrix}},\quad {\mbox{and}}\quad b={\begin{bmatrix}-I_{t}(q_{1})\\[10pt]-I_{t}(q_{2})\\[10pt]\vdots \\[10pt]-I_{t}(q_{n})\end{bmatrix}}](/2014-wikipedia_en_all_02_2014/I/media/3/3/e/c/33ec519f1943a440783c93b4ac98b4a4.png)
![{\begin{bmatrix}V_{x}\\[10pt]V_{y}\end{bmatrix}}={\begin{bmatrix}\sum _{i}I_{x}(q_{i})^{2}&\sum _{i}I_{x}(q_{i})I_{y}(q_{i})\\[10pt]\sum _{i}I_{y}(q_{i})I_{x}(q_{i})&\sum _{i}I_{y}(q_{i})^{2}\end{bmatrix}}^{{-1}}{\begin{bmatrix}-\sum _{i}I_{x}(q_{i})I_{t}(q_{i})\\[10pt]-\sum _{i}I_{y}(q_{i})I_{t}(q_{i})\end{bmatrix}}](/2014-wikipedia_en_all_02_2014/I/media/7/6/1/3/76131d763130942b287208d7378bcf5f.png)
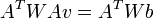
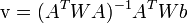
![{\begin{bmatrix}V_{x}\\[10pt]V_{y}\end{bmatrix}}={\begin{bmatrix}\sum _{i}w_{i}I_{x}(q_{i})^{2}&\sum _{i}w_{i}I_{x}(q_{i})I_{y}(q_{i})\\[10pt]\sum _{i}w_{i}I_{x}(q_{i})I_{y}(q_{i})&\sum _{i}w_{i}I_{y}(q_{i})^{2}\end{bmatrix}}^{{-1}}{\begin{bmatrix}-\sum _{i}w_{i}I_{x}(q_{i})I_{t}(q_{i})\\[10pt]-\sum _{i}w_{i}I_{y}(q_{i})I_{t}(q_{i})\end{bmatrix}}](/2014-wikipedia_en_all_02_2014/I/media/5/5/3/c/553c95e817bc4b32f43b2e883aede3b1.png)