Long Josephson junction
In superconductivity, a long Josephson junction (LJJ) is a Josephson junction which has one or more dimensions longer than the Josephson penetration depth  . This definition is not strict.
. This definition is not strict.
In terms of underlying model a short Josephson junction is characterized by the Josephson phase 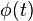 , which is only a function of time, but not of coordinates i.e. the Josephson junction is assumed to be point-like in space. In contrast, in a long Josephson junction the Josephson phase can be a function of one or two spatial coordinates, i.e.,
, which is only a function of time, but not of coordinates i.e. the Josephson junction is assumed to be point-like in space. In contrast, in a long Josephson junction the Josephson phase can be a function of one or two spatial coordinates, i.e., 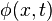 or
or 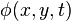 .
.
Simple model: the sine-Gordon equation
The simplest and the most frequently used model which describes the dynamics of the Josephson phase  in LJJ is the so-called perturbed sine-Gordon equation. For the case of 1D LJJ it looks like:
in LJJ is the so-called perturbed sine-Gordon equation. For the case of 1D LJJ it looks like:
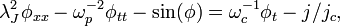
where subscripts  and
and 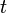 denote partial derivatives with respect to
denote partial derivatives with respect to  and
and 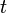 ,
,  is the Josephson penetration depth,
is the Josephson penetration depth, 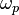 is the Josephson plasma frequency,
is the Josephson plasma frequency,  is the so-called characteristic frequency and
is the so-called characteristic frequency and 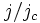 is the bias current density
is the bias current density  normalized to the critical current density
normalized to the critical current density 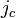 . In the above equation, the r.h.s. is considered as perturbation.
. In the above equation, the r.h.s. is considered as perturbation.
Usually for theoretical studies one uses normalized sine-Gordon equation:
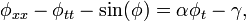
where spatial coordinate is normalized to the Josephson penetration depth  and time is normalized to the inverse plasma frequency
and time is normalized to the inverse plasma frequency 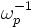 . The parameter
. The parameter  is the dimensionless damping parameter (
is the dimensionless damping parameter (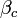 is McCumber-Stewart parameter), and, finally,
is McCumber-Stewart parameter), and, finally, 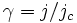 is a normalized bias current.
is a normalized bias current.
Important solutions
- Small amplitude plasma waves.
![\phi (x,t)=A\exp[i(kx-\omega t)]](/2014-wikipedia_en_all_02_2014/I/media/b/1/b/a/b1ba928c191bb9c3e651588902fc3fd5.png)
- Soliton (aka fluxon, Josephson vortex):[1]

Here  ,
, 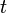 and
and 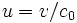 are the normalized coordinate, normalized time and normalized velocity. The physical velocity
are the normalized coordinate, normalized time and normalized velocity. The physical velocity  is normalized to the so-called Swihart velocity
is normalized to the so-called Swihart velocity  , which represent a typical unit of velocity and equal to the unit of space
, which represent a typical unit of velocity and equal to the unit of space  divided by unit of time
divided by unit of time 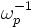 .
.
References
- ↑ M. Tinkham, Introduction to superconductivity, 2nd ed., Dover New York (1996).