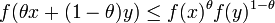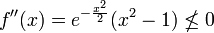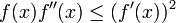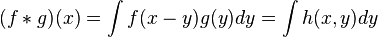Logarithmically concave function

From Wikipedia, the free encyclopedia

In convex analysis, a non-negative function $f : R n \to R +$ is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it satisfies the inequality

$f(\theta x+(1-\theta )y)\geq f(x)^{{\theta }}f(y)^{{1-\theta }}$

for all $x, y \in dom f$ and $0 < θ < 1$ . If $f$ is strictly positive, this is equivalent to saying that the logarithm of the function, $log \circ f$ , is concave; that is,

$\log f(\theta x+(1-\theta )y)\geq \theta \log f(x)+(1-\theta )\log f(y)$

for all $x, y \in dom f$ and $0 < θ < 1$ .

Examples of log-concave functions are the 0-1 indicator functions of convex sets (which requires the more flexible definition), and the Gaussian function.

Similarly, a function is log-convex if satisfies the reverse inequality

$f(\theta x+(1-\theta )y)\leq f(x)^{{\theta }}f(y)^{{1-\theta }}$

for all $x, y \in dom f$ and $0 < θ < 1$ .

Properties

A positive log-concave function is also quasi-concave.

Every concave function that is nonnegative on its domain is log-concave. However, the reverse does not necessarily hold. An example is the Gaussian function $f (x)$ = $exp(- x 2 /2)$ which is log-concave since $log f (x)$ = $- x 2 /2$ is a concave function of $x$ . But $f$ is not concave since the second derivative is positive for | $x$ | > 1:

$f''(x)=e^{{-{\frac {x^{2}}{2}}}}(x^{2}-1)\nleq 0$

A twice differentiable, nonnegative function with a convex domain is log-concave if and only if for all $x$ satisfying $f (x) > 0$ ,

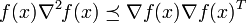$f(x)\nabla ^{2}f(x)\preceq \nabla f(x)\nabla f(x)^{T}$ , ^[1]

i.e.

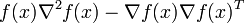$f(x)\nabla ^{2}f(x)-\nabla f(x)\nabla f(x)^{T}$ is

negative semi-definite. For functions of one variable, this condition simplifies to

$f(x)f''(x)\leq (f'(x))^{2}$

Operations preserving log-concavity

Products: The product of log-concave functions is also log-concave. Indeed, if $f$ and $g$ are log-concave functions, then $log f$ and $log g$ are concave by definition. Therefore

$\log \,f(x)+\log \,g(x)=\log(f(x)g(x))$

is concave, and hence also

f g

is log-concave.

Marginals: if $f (x, y)$ : $R n + m \to R$ is log-concave, then

$g(x)=\int f(x,y)dy$

is log-concave (see Prékopa–Leindler inequality).

This implies that convolution preserves log-concavity, since $h (x, y)$ = $f (x - y) g (y)$ is log-concave if $f$ and $g$ are log-concave, and therefore

$(f*g)(x)=\int f(x-y)g(y)dy=\int h(x,y)dy$

is log-concave.

Log-concave distributions

Log-concave distributions are necessary for a number of algorithms, e.g. adaptive rejection sampling.

As it happens, many common probability distributions are log-concave. Some examples:^[2]

The normal distribution and multivariate normal distributions.
The exponential distribution.
The uniform distribution over any convex set.
The logistic distribution.
The extreme value distribution.
The Laplace distribution.
The chi distribution.
The Wishart distribution, where n >= p + 1.^[3]
The Dirichlet distribution, where all parameters are >= 1.^[3]
The gamma distribution if the shape parameter is >= 1.
The chi-square distribution if the number of degrees of freedom is >= 2.
The beta distribution if both shape parameters are >= 1.
The Weibull distribution if the shape parameter is >= 1.

Note that all of the parameter restrictions have the same basic source: The exponent of non-negative quantity must be non-negative in order for the function to be log-concave.

The following distributions are non-log-concave for all parameters:

Note that the cumulative distribution function (CDF) of all log-concave distributions is also log-concave. However, some non-log-concave distributions also have log-concave CDF's:

The log-normal distribution.
The Pareto distribution.
The Weibull distribution when the shape parameter < 1.
The gamma distribution when the shape parameter < 1.

The following are among the properties of log-concave distributions:

If a density is log-concave, so is its cumulative distribution function (CDF).
If a multivariate density is log-concave, so is the marginal density over any subset of variables.
The sum of two log-concave random variables is log-concave. This follows from the fact that the convolution of two log-concave functions is log-concave.
The product of two log-concave functions is log-concave. This means that joint densities formed by multiplying two probability densities (e.g. the normal-gamma distribution, which always has a shape parameter >= 1) will be log-concave. This property is heavily used in general-purpose Gibbs sampling programs such as BUGS and JAGS, which are thereby able to use adaptive rejection sampling over a wide variety of conditional distributions derived from the product of other distributions.

Notes

↑ Stephen Boyd and Lieven Vandenberghe, Convex Optimization (PDF) p.105
↑ See Mark Bagnoli and Ted Bergstrom (1989), "Log-Concave Probability and Its Applications", University of Michigan.
↑ 3.0 3.1 András Prékopa (1971), "Logarithmic concave measures with application to stochastic programming". Acta Scientiarum Mathematicarum, 32, pp. 301–316.

References

Barndorff-Nielsen, Ole (1978). Information and exponential families in statistical theory. Wiley Series in Probability and Mathematical Statistics. Chichester: John Wiley \& Sons, Ltd. pp. ix+238 pp. ISBN 0-471-99545-2. MR 489333.

Dharmadhikari, Sudhakar; Joag-Dev, Kumar (1988). Unimodality, convexity, and applications. Probability and Mathematical Statistics. Boston, MA: Academic Press, Inc. pp. xiv+278. ISBN 0-12-214690-5. MR 954608.

Pfanzagl, Johann; with the assistance of R. Hamböker (1994). Parametric Statistical Theory. Walter de Gruyter. ISBN 3-11-013863-8. MR 1291393.

Pečarić, Josip E.; Proschan, Frank; Tong, Y. L. (1992). Convex functions, partial orderings, and statistical applications. Mathematics in Science and Engineering 187. Boston, MA: Academic Press, Inc. pp. xiv+467 pp. ISBN 0-12-549250-2. MR 1162312.