Logarithmic Schrödinger equation

From Wikipedia, the free encyclopedia

In theoretical physics, the logarithmic Schrödinger equation (sometimes abbreviated as LNSE or LogSE) is one of the nonlinear modifications of Schrödinger's equation. It is a classical wave equation with applications to extensions of quantum mechanics,[1] quantum optics,[2] nuclear physics,[3][4] transport and diffusion phenomena,[5][6] open quantum systems and information theory,[7][8][9][10][11][12] effective quantum gravity and physical vacuum models[13][14][15] and theory of superfluidity and Bose–Einstein condensation.[16] Its relativistic version (with D'Alembertian instead of Laplacian and first-order time derivative) was first proposed by G. Rosen.[17] It is an example of an integrable model.

The equation

The logarithmic Schrödinger equation is the partial differential equation. In mathematics and mathematical physics one often uses its dimensionless form:

i{\frac {\partial \psi }{\partial t}}+\Delta \psi +\psi \ln |\psi |^{2}=0.

for the complex-valued function 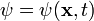\psi =\psi ({\mathrm {{\mathbf {x}}}},t). Here \Delta \, is the Laplacian with respect to the vector {\mathrm {{\mathbf {x}}}}.

The relativistic version of this equation can be obtained by replacing the derivative operator with the D'Alembertian, similarly to the Klein-Gordon equation.

See also

References

  1. ↑ I. Bialynicki-Birula and J. Mycielski, Annals Phys. 100, 62 (1976); Commun. Math. Phys. 44, 129 (1975); Phys. Scripta 20, 539 (1979).
  2. ↑ H. Buljan, A. Šiber, M. Soljačić, T. Schwartz, M. Segev, and D. N. Christodoulides, Phys. Rev. E 68, 036607 (2003).
  3. ↑ E. F. Hefter, Phys. Rev. A 32, 1201 (1985).
  4. ↑ V. G. Kartavenko, K. A. Gridnev and W. Greiner, Int. J. Mod. Phys. E 7 (1998) 287.
  5. ↑ S. De Martino, M. Falanga, C. Godano and G. Lauro, Europhys. Lett. 63, 472 (2003); S. De Martino and G. Lauro, in: Proceed. 12th Conference on WASCOM, 2003.
  6. ↑ T. Hansson, D. Anderson, and M. Lisak, Phys. Rev. A 80, 033819 (2009).
  7. ↑ K. Yasue, Quantum mechanics of nonconservative systems, Annals Phys. 114 (1978) 479.
  8. ↑ N. A. Lemos, Phys. Lett. A 78 (1980) 239.
  9. ↑ J. D. Brasher, Nonlinear wave mechanics, information theory, and thermodynamics, Int. J. Theor. Phys. 30 (1991) 979.
  10. ↑ D. Schuch, Phys. Rev. A 55, 935 (1997).
  11. ↑ M. P. Davidson, Nuov. Cim. B 116 (2001) 1291.
  12. ↑ J. L. Lopez, Phys. Rev. E. 69 (2004) 026110.
  13. ↑ K. G. Zloshchastiev, Logarithmic nonlinearity in theories of quantum gravity: Origin of time and observational consequences, Grav. Cosmol. 16 (2010) 288–297 ArXiv:0906.4282.
  14. ↑ K. G. Zloshchastiev, Vacuum Cherenkov effect in logarithmic nonlinear quantum theory, Phys. Lett. A 375 (2011) 2305–2308 ArXiv:1003.0657.
  15. ↑ K. G. Zloshchastiev, Spontaneous symmetry breaking and mass generation as built-in phenomena in logarithmic nonlinear quantum theory, Acta Phys. Polon. B 42 (2011) 261–292 ArXiv:0912.4139.
  16. ↑ A. V. Avdeenkov and K.G. Zloshchastiev, Quantum Bose liquids with logarithmic nonlinearity: Self-sustainability and emergence of spatial extent, J. Phys. B: At. Mol. Opt. Phys. 44 (2011) 195303 ArXiv:1108.0847.
  17. ↑ G. Rosen, Phys. Rev. 183 (1969) 1186.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.