Local flatness
In topology, a branch of mathematics, local flatness is a property of a submanifold in a topological manifold of larger dimension. In the category of topological manifolds, locally flat submanifolds play a role similar to that of embedded submanifolds in the category of smooth manifolds.
Suppose a d dimensional manifold N is embedded into an n dimensional manifold M (where d < n). If  we say N is locally flat at x if there is a neighborhood
we say N is locally flat at x if there is a neighborhood  of x such that the topological pair
of x such that the topological pair  is homeomorphic to the pair
is homeomorphic to the pair 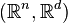 , with a standard inclusion of
, with a standard inclusion of  as a subspace of
as a subspace of  . That is, there exists a homeomorphism
. That is, there exists a homeomorphism 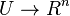 such that the image of
such that the image of  coincides with
coincides with  .
.
The above definition assumes that, if M has a boundary, x is not a boundary point of M. If x is a point on the boundary of M then the definition is modified as follows. We say that N is locally flat at a boundary point x of M if there is a neighborhood  of x such that the topological pair
of x such that the topological pair  is homeomorphic to the pair
is homeomorphic to the pair  , where
, where  is a standard half-space and
is a standard half-space and  is included as a standard subspace of its boundary. In more detail, we can set
is included as a standard subspace of its boundary. In more detail, we can set
 and
and 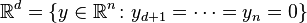 .
.
We call N locally flat in M if N is locally flat at every point. Similarly, a map  is called locally flat, even if it is not an embedding, if every x in N has a neighborhood U whose image
is called locally flat, even if it is not an embedding, if every x in N has a neighborhood U whose image  is locally flat in M.
is locally flat in M.
Local flatness of an embedding implies strong properties not shared by all embeddings. Brown (1962) proved that if d = n − 1, then N is collared; that is, it has a neighborhood which is homeomorphic to N × [0,1] with N itself corresponding to N × 1/2 (if N is in the interior of M) or N × 0 (if N is in the boundary of M).
See also
References
- Brown, Morton (1962), Locally flat imbeddings of topological manifolds. Annals of Mathematics, Second series, Vol. 75 (1962), pp. 331-341.