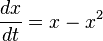Linear stability

From Wikipedia, the free encyclopedia

In mathematics, in the theory of differential equations and dynamical systems, a particular stationary or quasistationary solution to a nonlinear system is called linearly or exponentially unstable if the linearization of the equation at this solution has the form 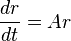{\frac {dr}{dt}}=Ar, where A is a linear operator whose spectrum contains points with positive real part. If there are no such eigenvalues, the solution is called linearly, or spectrally, stable.

Example 1: ODE

The differential equation

{\frac {dx}{dt}}=x-x^{2}

has two stationary (time-independent) solutions: x = 0 and x = 1. The linearization at x = 0 has the form {\frac {dx}{dt}}=x. The solutions to this equation grow exponentially; the stationary point x = 0 is linearly unstable.

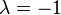To derive the linearizaton at x = 1, one writes {\frac {dr}{dt}}=(1+r)-(1+r)^{2}=-r-r^{2}, where r = x − 1. The linearized equation is then {\frac {dr}{dt}}=-r; the linearized operator is A = −1, the only eigenvalue is \lambda =-1, hence this stationary point is linearly stable.

Example 2: NLS

The nonlinear Schrödinger equation

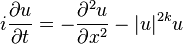i{\frac {\partial u}{\partial t}}=-{\frac {\partial ^{2}u}{\partial x^{2}}}-|u|^{{2k}}u, where u(x,t) ∈ ℂ and k > 0,

has solitary wave solutions of the form \phi (x)e^{{-i\omega t}} .[1] To derive the linearization at a solitary wave, one considers the solution in the form u(x,t)=(\phi (x)+r(x,t))e^{{-i\omega t}}. The linearized equation on r(x,t) is given by

{\frac {\partial }{\partial t}}{\begin{bmatrix}{\text{Re}}\,u\\{\text{Im}}\,u\end{bmatrix}}=A{\begin{bmatrix}{\text{Re}}\,u\\{\text{Im}}\,u\end{bmatrix}},

where

A={\begin{bmatrix}0&L_{0}\\-L_{1}&0\end{bmatrix}},

with

L_{0}=-{\frac {\partial }{\partial x^{2}}}-k|u|^{2}-\omega

and

L_{1}=-{\frac {\partial }{\partial x^{2}}}-(2k+1)|u|^{2}-\omega

the differential operators. According to Vakhitov–Kolokolov stability criterion ,[2] when k > 2, the spectrum of A has positive point eigenvalues, so that the linearized equation is linearly (exponentially) unstable; for 0 < k ≤ 2, the spectrum of A is purely imaginary, so that the corresponding solitary waves are linearly unstable.

It should be mentioned that linear stability does not automatically imply stability; in particular, when k = 2, the solitary waves are unstable. On the other hand, for 0 < k < 2, the solitary waves are not only linearly stable but also orbitally stable.[3]

See also

References

  1. ↑ H. Berestycki and P.-L. Lions (1983). "Nonlinear scalar field equations. I. Existence of a ground state". Arch. Rational Mech. Anal. 82: 313–345. Bibcode:1983ArRMA..82..313B. doi:10.1007/BF00250555. 
  2. ↑ N.G. Vakhitov and A.A. Kolokolov (1973). "Stationary solutions of the wave equation in the medium with nonlinearity saturation". Radiophys. Quantum Electron. 16: 783–789. Bibcode:1973R%26QE...16..783V. doi:10.1007/BF01031343. 
  3. ↑ Manoussos Grillakis, Jalal Shatah, and Walter Strauss (1987). "Stability theory of solitary waves in the presence of symmetry. I". J. Funct. Anal. 74: 160–197. doi:10.1016/0022-1236(87)90044-9. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.